hopkinmn
- 22
- 0
Homework Statement
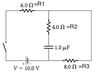
The capacitor is initially uncharged when the switch is closed for a long time. Calculate the current through R2.
Then find the potential difference across R1, R2, and R3
Homework Equations
V=IR
Iin=Iout
The Attempt at a Solution
I first set up current going into top node (I1) equal to the sume of the currents leaving that node (I2 and I3). So I1=I2+I3. I set voltage of the battery equal to V.
Then, I used Kirchoff's rules and the following equations 0=-R1*I1-R3*I3+V and R3*I3=R2*I2 to get I2=10/13, I3=5/13, and I1=15/13.
For the potential differences I found V2=V3=40/13V and V1=90/13V
So the sum of the potential differences across the resistors is equal to the voltage on the battery.
But if this is true, that means that the capacitor does not have a potential difference. But is this true? Or would there be no voltage on R2 and instead have voltage on the capacitor?