Calculate E Field at x=6m | Graph E Field in x Direction from -3m to 11m

[pyroknife]

Homework Statement

2 charges of 4x10^-6 C are located at the origin and at x=8m y=0m.
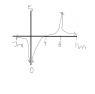
Find the E field at x=6m. and graph the e field in the x direction with respect to x from -3m<x<11m

Homework Equations

E=kq/r

The Attempt at a Solution

sorry, idk how to use subscripts. If you see a number after a letter that means its a sub, E1 is for the charge at the origin.
E=E1-E2=kq1/r1^2 - kq2/r2^2
=(9x10^9)(4x10^-6)/2^2 - (9x10^9)(4x10^-6)/6^2= -8000 N/C


I attached my graph sorry for a crappy paint drawing. The curves should be more rounded.

 

[lightgrav]

no, (1) the E-field is a vector, with direction away from positive charges.
(2) the "r" in the denominator (that is squared) is the distance from charge to field point.
so, is 2m for one charge, and 6m for the other charge.

 

[pyroknife]

no, (1) the E-field is a vector, with direction away from positive charges.
(2) the "r" in the denominator (that is squared) is the distance from charge to field point.
so, is 2m for one charge, and 6m for the other charge.

I don't understand what you mean with (1). and for (2) isn't 2 and 6 what I had for the 2 r's?

 

[Dick]

I don't understand what you mean with (1). and for (2) isn't 2 and 6 what I had for the 2 r's?

lightgrav is right about the vector part. Think about just E=kq/x^2 for q>0. If you plot that you get that E is positive on both sides of 0 like your graph shows. That's not right. The E field is negative on the left side of x=0 and positive on the right side of x=0. You put the 'vector' part in by hand to get the right answer by adjusting signs at x=6. You didn't adjust the signs in the general case of any x. Your graph doesn't even show a negative E field at x=6.

 

[pyroknife]

lightgrav is right about the vector part. Think about just E=kq/x^2 for q>0. If you plot that you get that E is positive on both sides of 0 like your graph shows. That's not right. The E field is negative on the left side of x=0 and positive on the right side of x=0. You put the 'vector' part in by hand to get the right answer by adjusting signs at x=6. You didn't adjust the signs in the general case of any x. Your graph doesn't even show a negative E field at x=6.

oh ok i think I see what you're saying. I got the -8000 N/C right though right? For the graph, my left, and right ones are right, but the middle one is opposite right? As in, for my middle plot the graph should be approaching positive infinity at x=0 from the right and approaching negative negative from the left at x=8?

 

[Dick]

oh ok i think I see what you're saying. I got the -8000 N/C right though right? For the graph, my left, and right ones are right, but the middle one is opposite right? As in, for my middle plot the graph should be approaching positive infinity at x=0 from the right and approaching negative negative from the left at x=8?

Yes, that sounds right. You can also write the field kq/x^2 as kqx/|x|^3 which always gets the sign right without putting it in by hand and also works for vectors. Do you see why?

 

[pyroknife]

Yes, that sounds right. You can also write the field kq/x^2 as kqx/|x|^3 which always gets the sign right without putting it in by hand and also works for vectors. Do you see why?

Yes I think so, the adding the x in the numerator will make the sign match the positive/negative distance, idk how to word it right.

 

[Dick]

Yes I think so, the adding the x in the numerator will make the sign match the positive/negative distance, idk how to word it right.

Good enough. If you think of v as a vector then kqv/|v|^3 will always have the same magnitude as kq/v^2 but it will point in the direction of v, like it's supposed to.