Moment of inertia about y-axis by direct integration

[stinlin]

Homework Statement

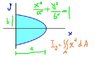
Determine by direct integration the moment of inertia about the y-axis in the figure shown.

Homework Equations

See Iy on attached.
Equation for curve also on attached.

The Attempt at a Solution

My answer didn't include pi, and the answer apparently does. I'm trying to do this via a double integral as opposed to using one integral and doing something funky. My problem I THINK is in finding dA.

 

[HallsofIvy]

You are right. There is no "$\pi$" in the solution.

The moment of inertia of that figure, about the y-axis is
$$\int_{x=0}^a\int_{y= -b\sqrt{1-\frac{x^2}{a^2}}}^{b\sqrt{1-\frac{x^2}{a^2}}} y dydx$$
That's easy to integrate and has no "$\pi$".

 

[stinlin]

Hmm - that's what I thought. In fact, I think that's the exact integral that I had. I'll give it another go. Thanks!

 

[stinlin]

I lied - that's a y^2, not just a y in the integral. The answer is pi*a*(b^3)/8...Still no luck though.