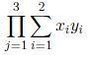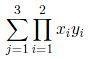You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Calculate Sum of Products (x,y,z)
- Thread starter tstuddud
- Start date
-
- Tags
- Sum
AI Thread Summary
The discussion centers on calculating the sum of products using the arrays x=(-3,2,5), y=(2,4,-5), and z=(1,6,7). The method involves performing an inner summation of products followed by an outer product operation. Clarifications are made regarding the formulas presented, with emphasis on ensuring the correct interpretation of the summation and product indices. The calculations yield results of 24 and 144 for the two different interpretations of the formulas. Understanding the correct application of these operations is crucial for solving such problems effectively.
Physics news on Phys.org
NJunJie
- 33
- 0
I view such qns playing with 'arrays' and 'susbstituion'.
Generally, i will view it this way:-
x is an array of (-3,2,5)
y is an array of (2,4,-5)
first part is u do the summation first - i call it inner.
Inner: (-3)(2) + (2)(4)
Then you do the Products - i call it outer.
But is your question complete? Theres no 'j' in your formulaes pasted.
Generally, i will view it this way:-
x is an array of (-3,2,5)
y is an array of (2,4,-5)
first part is u do the summation first - i call it inner.
Inner: (-3)(2) + (2)(4)
Then you do the Products - i call it outer.
But is your question complete? Theres no 'j' in your formulaes pasted.
HallsofIvy
Science Advisor
Homework Helper
- 42,895
- 984
tstuddud said:I don't quite understand the method to solve this type of question.
Let x=(-3,2,5), y=(2,4,-5), and z=(1,6,7). Calculate:
What you have written,
\prod_{j= 1}^3\sum_{i=1}^2 x_iy_i and
\sum_{j=1}^3\prod_{i=1}^2 x_iy_i
are just
\prod_{j=1}^3(x_1y_1+ x_2y_2+ x_3y_3)= \prod_{j=1}^3((-3)(2)+ (2)(4)+ (5)(-5))= \prod_{j=1}^3(-6+ 8- 10)= 3(8)= 24
and
\sum{j= 1}^3((x_1y_1)(x_2y_2))= \sum_{j=1}^3 (-3)(2)(2)(4)= \sum_{j=1}^3 48= 3(48)= 144
But I suspect you meant
\prod_{j=1}^3\sum_{i= 1}^2 x_iy_j and
\sum{j=1}^3\Pi_{i=1}^2 x_iy_j
The first of those is
\prod_{j=1}^3(x_1+ x_2)y_j= (x_1+ x_2)\prod_{j=1}^3y_i= (x_1+ x_2)(y_1y_2y_3)
surely you can do that arithmetic yourself.
I tried to combine those 2 formulas but it didn't work. I tried using another case where there are 2 red balls and 2 blue balls only so when combining the formula I got ##\frac{(4-1)!}{2!2!}=\frac{3}{2}## which does not make sense.
Is there any formula to calculate cyclic permutation of identical objects or I have to do it by listing all the possibilities?
Thanks
Similar threads
- Replies
- 5
- Views
- 1K
- Replies
- 11
- Views
- 2K
- Replies
- 19
- Views
- 2K
- Replies
- 8
- Views
- 2K
- Replies
- 17
- Views
- 2K
- Replies
- 17
- Views
- 3K
- Replies
- 14
- Views
- 3K
- Replies
- 52
- Views
- 4K
- Replies
- 3
- Views
- 1K
- Replies
- 5
- Views
- 2K
Hot Threads
-
Geometry: Similar Shapes
- Started by paulb203
- Replies: 116
- Precalculus Mathematics Homework Help
-
[ASK] Trigonometric Inequality
- Started by Monoxdifly
- Replies: 6
- Precalculus Mathematics Homework Help
-
What does this equation mean?
- Started by inuka00123
- Replies: 12
- Precalculus Mathematics Homework Help
-
Finding polar equation of a shifted cricle
- Started by farfromdaijoubu
- Replies: 6
- Precalculus Mathematics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math