Calculate the charge flowing in the coil if the field is removed

[Bolter]

Homework Statement

Calculate the charge flowing in the coil if the magnetic field is removed

Relevant Equations

Faraday's law

Hello

So here is my question

Not so sure how to approach this question

This is what I have worked out so far which is the magnetic field strength of the solenoid, not sure if this comes in helpful though

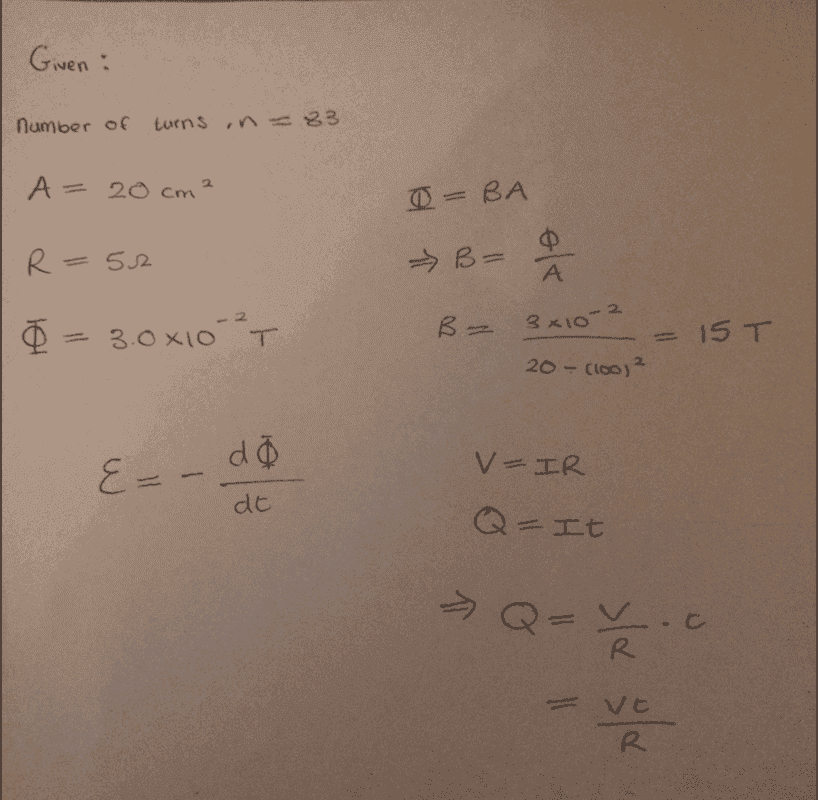
Thanks for any help!

 

[kuruman]

Ignoring the negative sign, start with $I=\dfrac{1}{R}\dfrac{d\Phi}{dt}$.
Then integrate $dQ=Idt$.

 

[Bolter]

Ignoring the negative sign, start with $I=\dfrac{1}{R}\dfrac{d\Phi}{dt}$.
Then integrate $dQ=Idt$.

I'm not so sure about the integrate part

I know that charge Q is I*t, and I used that expression of I that was used before to sub into the integration step giving me this

 

[kuruman]

I'm not so sure about the integrate part

Be sure. Just write it out and see what you get. Q=I*t only if I is constant in time.

 

[Bolter]

Be sure. Just write it out and see what you get. Q=I*t only if I is constant in time.

Ok this is most likely wrong :( but I got this when I write it out

I know previously that the magnetic field strength is 15 T from using magnetic flux linkage = BA earlier on

 

[kuruman]

Yes, you did it wrong. You should know better than to cancel $t$ in the numerator with $dt$ in the denominator. At least you didn't cancel only the $t$'s and leave the $d$ in the denominator. .

You didn't do what I asked you to do, namely write out the integral.$$\int dQ=\int Idt=\frac{1}{R}\int\frac{d\Phi}{dt}dt=?$$You know the left hand side integrates to the total charge $Q$. What does the right hand side integrate to and why?

 

[Bolter]

Yes, you did it wrong. You should know better than to cancel $t$ in the numerator with $dt$ in the denominator. At least you didn't cancel only the $t$'s and leave the $d$ in the denominator. .

You didn't do what I asked you to do, namely write out the integral.$$\int dQ=\int Idt=\frac{1}{R}\int\frac{d\Phi}{dt}dt=?$$You know the left hand side integrates to the total charge $Q$. What does the right hand side integrate to and why?

So right hand side integrates to this?

But we aren't given a value of time in the question so how can this help us?

 

[TSny]

You can cancel the two dt's here:

Also, note that the magnetic field B is given to be .03 T, it is not 15 T.
Φ is "flux", B is "flux density".

 

[kuruman]

You can cancel the two dt's here:

View attachment 257296

Also, note that the magnetic field B is given to be .03 T, it is not 15 T.
Φ is "flux", B is "flux density".

Thank you.

 

[Bolter]

You can cancel the two dt's here:

View attachment 257296

Also, note that the magnetic field B is given to be .03 T, it is not 15 T.
Φ is "flux", B is "flux density".

So if the two dt's cancel each other out.

That should mean that the total charge flowing is 1/R * (change of flux)?

 

[Bolter]

You can cancel the two dt's here:

View attachment 257296

Also, note that the magnetic field B is given to be .03 T, it is not 15 T.
Φ is "flux", B is "flux density".

I get 0.996 millicoulombs to be my answer?

 

[TSny]

I get 0.996 millicoulombs to be my answer?

OK. The data is given to 2 significant figures (except for R). What is your answer to 2 significant figures?

 

[Bolter]

OK. The data is given to 2 significant figures (except for R). What is your answer to 2 significant figures?

It would be 1.00 mC to 2 sig figs

 

[TSny]

It would be 1.00 mC to 2 sig figs

That's 3 significant figures

 

[Bolter]

That's 3 significant figures

Ok so 1.0 mC , I thought you had to discount the first zero to begin with in 0.996, my mistake