Calculate the current through the 22ohm resistor (Kirchhoff's Rules)

[shashaeee]

From the image attached:

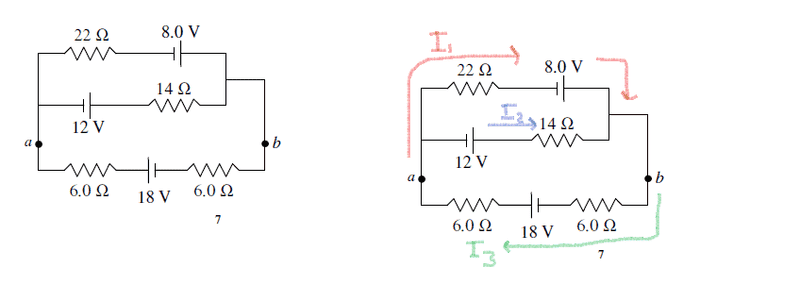
A. Calculate the current through the 22Ω resistor.
B. What is the voltage across ab


Here is what I've done:
A. )
I labelled the currents and applied the Junction Rule
I1 + I2 = I3

-I1*22Ω + 8V + 13*6Ω + 18V - I3*6Ω = 0
-I1*22Ω + 8V + I2*14Ω - 12V = 0

Which I rearrange into:

2.17A - I1*1.83 = I3 and

I2 = 0.29A + I1*1.57

Inserting these two equations into I1 + I2 = I3

I1 = (2.17A - I1*1.83) - (0.29A + I1*1.57)
I1 = 0.43A

I3 = 2.17A - (0.43A)*1.83
I3 = 1.38A

I2 = 0.29A + (0.43A)*1.57
I2 = 0.96A

Therefore the current through the 22Ω will be 0.43A ?



B.) For this question, I really don't know how to tackle this, do I just do V=I3*R + 18v ?

For R, do I just add up the resistors (6Ω + 6Ω) in series?

 

[TSny]

-I1*22Ω + 8V + 13*6Ω + 18V - I3*6Ω = 0
-I1*22Ω + 8V + I2*14Ω - 12V = 0

In the first equation above, the third term would be -I3*6 rather than +I3*6, but I think that's what you meant. Your work following that looks correct, and your answers for the currents look correct.

B.) For this question, I really don't know how to tackle this, do I just do V=I3*R + 18v ?

For R, do I just add up the resistors (6Ω + 6Ω) in series?

You want to think of starting at point a and going by any path to point b and add up the voltage changes along the path. Looks like you chose a path along the bottom leg. Yes, you can add the two 6Ω resistors because they are in series. But note that as you go from a to b, you go from the + terminal to the - terminal of the battery. So, that's a negative change of -18V. See what you get and then try a couple of other paths from a to b and see if you get the same answer. Keep in mind that when you go through a resistor in a direction opposite to the current, the voltage change is positive.

 

[shashaeee]

Thank you for your response!

So I tried two ab paths: through the I1 current and the I3 current

This is what I've gotten:

Vab (bottom) = I3*(6Ω+6Ω) - 18v = -1.40v
Vab (top) = -I1*22Ω +8v = -1.40v

 

[SammyS]

Thank you for your response!

So I tried two ab paths: through the I1 current and the I3 current

This is what I've gotten:

Vab (bottom) = I3*(6Ω+6Ω) - 18v = -1.40v
Vab (top) = -I1*22Ω +8v = -1.40v

That looks close to the correct answer. No doubt there's some round off error.

See this link for the same problem a couple of weeks ago: Find the current and the voltage; the Circuit Problem