Jorgen1224
- 36
- 0
Homework Statement
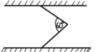
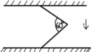
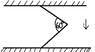
There is a metal stick that is connected to the ceiling with another one. The angle between them is 60°. Calculate the friction.
Both lengths and weights are the same.
Homework Equations
T = f N
or actually none, except trygonometry
The Attempt at a Solution
I tried using this equation T = f N and convert it somehow, but i bet that trygonometry is strictly required here, but i don't really know how to use it. So I'm asking for any tips that could help me out.
I see that if we cut this structure in a half then we have 2 equal rectangular triangles with angles: 30, 60 and 90. And i don't really know what am i supposed to do next
Sorry for inaccuracies, because scientific english is quite new for me.
------------------
Actually i made a new thread, because in the last one i made a huge mistake, i simply meant friction but I wrote tension
 Sorry for those who attempted at my problem and tried to understand what i meant.
Sorry for those who attempted at my problem and tried to understand what i meant.Attachments
Last edited: