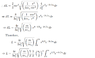A Calculate the moment of inertia of H with the probability from wavefunction

[fisher garry]

the spin, S, for an electron is

$$\frac{\hbar}{2}=5.27 \cdot 10^{-35} $$

$$\frac{2MR^2 \omega}{5}=\frac{2MRv}{5}$$

It is said that the speed of an electron is 2200 km per second and can be calculated in classical manners from electrostatic and accelerating forces on the electron

from (1.11) the spin is $$\frac{2MRv}{5}=\frac{2 \cdot 9.1 \cdot 10^{-31} \cdot 5.291 \cdot 10^{-11} \cdot 2200 \cdot 10^{3}}{5}=4.23 \cdot 10^{-35} $$

It is almost the same. Is this just from approximation errors? My problem is also that I have used bohr radius which is calculated by quantum physics rules not classical rules as far as I know? And since this is based on moment of inertia of a sphere one must use an R that is larger then the minimum R which I use the only problem is that electron cloud of the electron is not evenly distributed so where would one set this R? And since we are looking for an outer R and we are not looking for v in the outer R we can use an average v which could lead to a more precise relation of Plancks constant?

 

[fisher garry]

I am trying to calculate moment of inertia of an H electron by using the wavefunction. But I believe my value is wrong. Can anyone help out?

 

[dextercioby]

What is the purpose of this calculation and what theoretical formulas do you use?

 

[fisher garry]

[mentor's note: The post mentioned here has been moved into this thread, #2]

Look at this question:

https://www.physicsforums.com/threads/calculating-electron-spin-from-calculus.916722/

I wanted to get a better approximation for spin,S, by calculating a new radius R. In the question from the link I used bohr radius but the model uses a sphere with evenly charge distribution as an approximation for the electron which of course is not compatible with the real hydrogen electron cloud

 

[fisher garry]

I have tried to expand this to calculation of E=hf. In NMR $$E=hf$$ The larmor frequency seems to be derived from classical and EM physics. $$\gamma B$$ Which would lead to by classical reasoning: $$\Delta E=\gamma \hbar B_0$$ The problem is that this is the differnce in spin: $$S=\hbar /2$$ and then they also use that the lower spin value is $$S=-\hbar /2$$ So that they obtain $$\Delta E=hf=\hbar \omega_0=0.5\hbar\gamma B_0-(-0.5\hbar \gamma B_0)=\hbar \gamma B_0$$

But my classical approximation of spin is $$\hbar/2$$. Would anyone come to think of a way to get a minus sign for the spin in the derivation above in my first post? What if I turn the current in the first post derivation all in the top of this thread? And keeping in mind that hf is created from acceleration and that particles shed out hf as they are accelerated?Really an analogy to breaks on a car and that energy is conserved when a car stops from deacceleration.

 

[fisher garry]

It is actually possible to calculate orbital angular momentum classically for m=1 also:

$$L=mrv=9.1\cdot10^{-31}\cdot 5.291\cdot 10^{-11}\cdot 2200\cdot 10^3=1.059\cdot 10^{-34}$$

Wheras orbital angular momentum for m=1 is:

$$\hbar=1.054\cdot10^{-34}$$

 

[ivy]

Is the wave function valid? Before you do all these derivations. Also, Planck's constant represents the energy of light and cannot be used to represent matter that has a real mass, like an electron or proton..atom...etc. etc.

 

[fisher garry]

Is the wave function valid? Before you do all these derivations. Also, Planck's constant represents the energy of light and cannot be used to represent matter that has a real mass, like an electron or proton..atom...etc. etc.

My understanding: Planck's constant is most often seen in quantum mechanics but the coincident was that as I calculated the spin by integrating $L=I\omega$ over a spherical electron model the number came very close to $\hbar/2$. Then that would explain how the angular momentum that leads to rotational energy is called $\hbar/2$ and further $\Delta E=\frac{q}{2m}S_1B-(\frac{q}{2m}S_2B)=\frac{q}{2m}\frac{\hbar}{2}B-(\frac{q}{2m}\frac{-\hbar}{2}B)=\frac{q}{2m}\frac{\hbar}{1}B=\gamma\hbar B$. And this is by using that spin is $\hbar/2$ as derived in the first post only classical reasoning. What is not classical however is that as explained in Stern Gerlach: the spin goes on of two distinct ways. But the classical calculation of spin that I did shows that spin is proportional to velocity of the electron and a 180 degrees turn in spin leads to emittion of the energy described above. So if you use this 180 degrees constraint, the rest is classical reasoning. As an attempt to answer your second notion: The $\Delta E$ is energy when it is emitted as E=hf from deacceleration of the electron as derived in post 5 in this thread. And that was how I got from classical reasoning to the emission of the particleless photon that in vacuum has the speed of light. Note that photons are defined as being emitted when particles deaccelerate.

I wanted to skip the wave function as it is from Schrødinger's equation and it would lead to circular reasoning. The cirular reasoning problem for me is explained like this: I wanted to prove the excistence of Planck' constant in quantum physics by using classical reasoning and going through schrødinger's equation which I have proved with the usage of $E=hf=0.5mv^2=mc^2$ would then be circular reasoning for me since I by thoose equalities have assumed that I can use the Planck's constant in E=hf

 

[PeterDonis]

I wanted to prove the excistence of Planck' constant in quantum physics by using classical reasoning

Which can't be done. You can find plenty of coincidences, but that is not the same as a proof.

Thread closed.