Alex Katko
- 15
- 0
Homework Statement
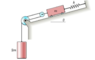
Calculate the natural circular frequency ωn of the system shown in the figure. The mass and friction of the pulleys are negligible. The diagram is attached.
Homework Equations
ωn = (k/m)1/2
The Attempt at a Solution
I can see the total mass of the system is 3m. So in the equation instead of m, the equivalent mass of the system is 3m. The equivalent k is giving me some difficulties. I know that is has to do with x (the spring deflection) and how it relates to the system.
My thought was that if the spring moves x meters down the slope, then the larger mass (2m) will move only 1/2*x meters down. Thus, my solution was ωn = [(k/2)/(3m)]1/2 or ωn = (k/6m)1/2
The correct answer is ωn = 1/3*(k/m)1/2