Calculate the work done according to the graph.

In summary, the task was to calculate the work done by a gas as it expands from point A to point B on the pV diagram shown. The equation used was Work=PΔV, and the attempt at a solution involved calculating the area under the curve and adding both areas together. The calculated answer was 8*10^11 J, but the correct answer was 800J. There may have been an error in converting units from liters to cubic meters.
  • #1
ScienceGeek24
164
0

Homework Statement



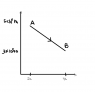
Calculate the work done by a gas as it slowly expands from point A to point B on the pV diagram shown.

Homework Equations


Work=PΔV


The Attempt at a Solution



I calculatate the area under the curve and added both of the areas and I came up with 8*10^11 J and the answer sheet is saying 800J Now i really don't why I am getting the wrong asnwer if I'm doing everything step by step.
 

Attachments

  • pv diagrzm.png
    pv diagrzm.png
    4.7 KB · Views: 478
Physics news on Phys.org
  • #2
Hi ScienceGeek24! :smile:

(try using the X2 button just above the Reply box :wink:)

Your method is correct, but you seem to be saying that litre is 106 cubic metres. :biggrin:
 

FAQ: Calculate the work done according to the graph.

What is the formula for calculating work on a graph?

The formula for calculating work on a graph is W = F x d, where W is work, F is force, and d is displacement.

How do you find the force from a graph?

To find the force from a graph, you can look at the slope of the line. The steeper the slope, the greater the force.

What does the area under the graph represent?

The area under the graph represents the work done. It is equal to the force multiplied by the distance.

Can you calculate work if the graph is not a straight line?

Yes, you can calculate work even if the graph is not a straight line. In this case, you would need to divide the graph into smaller sections and calculate the work for each section, then add them together to get the total work.

How is work calculated if the graph is in a different unit of measurement?

If the graph is in a different unit of measurement, you would need to convert the units to match the work formula (W = F x d). For example, if the graph is in meters and Newtons, you would need to convert the distance to meters and the force to Newtons before calculating work.

Similar threads

Help Calculate Work Done in Adiabatic Process & Fill Table
Replies
19
Views
2K
Calculating work done by a gas
Replies
2
Views
413
Confusion about work done by a gas - Thermodynamics
Replies
15
Views
714
Thermodynamics, find the work done from the graph
Replies
8
Views
5K
Conceptual misunderstanding in applying formula for work done in adiabatic compression
Replies
10
Views
898
What mistake am I making when calculating work done by a force?
Replies
6
Views
1K
Finding Work done under a graph?
Replies
13
Views
2K
Calculating the work done in a PV diagram
Replies
5
Views
2K
What Must Remain Constant for W = pΔV to Apply?
Replies
9
Views
3K
Is My Calculation of Work Along a Defined Curve Correct?
Replies
4
Views
439

Hot Threads

Recent Insights

Back
Top