RanTanPlan
- 12
- 0
<< Mentor Note -- thread moved to the schoolwork forums after we found out this is really a homework assignment >>[/color]
Hi,
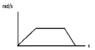
I've got a cylinder which needs to turn 90 deg. clockwise and 90 deg. counterclockwise (seen below from the front and above). How do I calculate the necessary torque on the engine? I can disregard the weight of the bracket holding the cylinder. Any help would be much appriciated!


Hi,
I've got a cylinder which needs to turn 90 deg. clockwise and 90 deg. counterclockwise (seen below from the front and above). How do I calculate the necessary torque on the engine? I can disregard the weight of the bracket holding the cylinder. Any help would be much appriciated!
Attachments
Last edited by a moderator:

 and you already replied.
and you already replied. 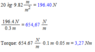
 , sorry. 1 second is a lot better. In that one second, it has to accelerate from standstill, and decelerate to standstill again,as
, sorry. 1 second is a lot better. In that one second, it has to accelerate from standstill, and decelerate to standstill again,as