You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Calculating Acceleration with Tension: A Troubleshooting Guide
- Thread starter user5
- Start date
-
- Tags
- Acceleration Tension
AI Thread Summary
The discussion focuses on troubleshooting calculations related to acceleration and tension in a physics problem. Participants clarify that the original calculations were incomplete due to the incorrect use of angles in the tangent function. They emphasize the importance of correctly identifying the sides of the triangle in relation to the angle α. The conversation also touches on the implications of infinite acceleration in real-world scenarios and the dependency of acceleration on the angle when force remains constant. Overall, the thread highlights the need for precise mathematical modeling in physics problems.
Physics news on Phys.org
voko
- 6,053
- 391
You did not go wrong anywhere, but you did not finish. You have some angle in your formula, while the expected result does not have any.
user5
- 38
- 0
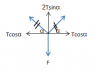
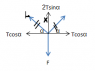
I have Tx=(FCOSα)/(2SINα)=(F)/(2TANα)=[F(L2-X2)0.5)]/2X
I have the wrong answer:(
I have the wrong answer:(
voko
- 6,053
- 391
You obviously used the wrong sides of the triangle to compute the tangent function. Think about that again. If you come to the same result again, post your thoughts here, and we will discuss.
voko
- 6,053
- 391
Which side is x? How is it related with the angle?
voko
- 6,053
- 391
x is the perpendicular distance from the line of F. Is that the case on your diagram?
user5
- 38
- 0
Thus it is going to be tanα=(L2-X2)0.5/X? With 2Tsinα=F it seems to give the right answer, however in the "student solution" they refer to that problem as having 2Tcosα=F, Am I right this time?
Does it matter where I decide to place α ?
Does it matter where I decide to place α ?
Last edited:
user5
- 38
- 0
1. From the start x=L thus is the acceleration infinite?
2. Is ax changing while F is constant?
2. Is ax changing while F is constant?
Cbray
- 130
- 0
The notation in your working hurts my brain.
voko
- 6,053
- 391
user5 said:Thus it is going to be tanα=(L2-X2)0.5/X? With 2Tsinα=F it seems to give the right answer, however in the "student solution" they refer to that problem as having 2Tcosα=F, Am I right this time?
Does it matter where I decide to place α ?
Obviously, there are two angles that you can use, but the end result should be the same.
user5 said:1. From the start x=L thus is the acceleration infinite?
Nothing ever gets infinite in the real world. If you get something infinite in a problem, that means that its mathematical model becomes invalid.
2. Is ax changing while F is constant?
It depends on the angle, so, yes.
user5
- 38
- 0
voko, I'm grateful to you for your help!
Similar threads
- Replies
- 38
- Views
- 4K
- Replies
- 4
- Views
- 1K
- Replies
- 12
- Views
- 523
- Replies
- 22
- Views
- 384
- Replies
- 19
- Views
- 1K
- Replies
- 23
- Views
- 2K
- Replies
- 14
- Views
- 1K
- Replies
- 10
- Views
- 2K
- Replies
- 43
- Views
- 4K
- Replies
- 39
- Views
- 2K
Hot Threads
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
-
How do you calculate the pull of this piston?
- Started by vdance
- Replies: 27
- Introductory Physics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math