ultrapoci
- 1
- 0
- Homework Statement
- Draw the Feynman diagrams contributing to the process ##\mu^+ \mu^- \rightarrow H + H## at the lowest electroweak order and calculate the squared amplitude
- Relevant Equations
- Vertex of the Feynman diagrams between two fermions and the Higgs boson is ##i\frac{m}{v}##, and the triple interaction vertex of the Higgs boson is ##i \lambda v## where ##m## is the muon's mass, ##v## is the vacuum expectation value of the Higgs boson, and ##\lambda## is its coupling constant.
Hi! I'd like to ask you if my calculation of the amplitude on the mentioned process in the Standard Model is correct. The three diagrams contributing at lowest order should be
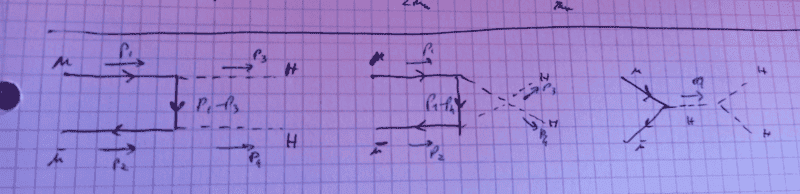
where in the middle one the two Higgs boson are NOT forming a quartic interaction vertex.
My attempt at calculating the (not yet squared) amplitude is this: $$A = \bar{v}(p_2) \left( \frac{im}{v} \frac{i}{\gamma^\mu(p_1-p_3)_\mu} \frac{im}{v} + \frac{im}{v} \frac{i}{\gamma^\mu(p_1-p_4)_\mu} \frac{im}{v} + \frac{im}{v} \frac{i}{q^2 - M_H^2 +i\Gamma_H M_H} i \lambda v \right) u(p_1)$$ Is this right?
where in the middle one the two Higgs boson are NOT forming a quartic interaction vertex.
My attempt at calculating the (not yet squared) amplitude is this: $$A = \bar{v}(p_2) \left( \frac{im}{v} \frac{i}{\gamma^\mu(p_1-p_3)_\mu} \frac{im}{v} + \frac{im}{v} \frac{i}{\gamma^\mu(p_1-p_4)_\mu} \frac{im}{v} + \frac{im}{v} \frac{i}{q^2 - M_H^2 +i\Gamma_H M_H} i \lambda v \right) u(p_1)$$ Is this right?