Calculating Angular Velocity and Tensions After a Ball Hits a Board at an Angle

[Raphael30]

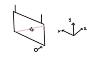
For a question involving a ball hitting orthogonally the bottom corner of a board held by wires, I need to calculate the angular velocity of the board and ball (collision is inelastic) right after the collision, before there's any external torque.

I can easily calculate the angular momentum L, equal to the momentum of the ball x its distance from the combined center of mass at the moment of collision. I could then find w using L=wI, but integrating the moment of inertia for a rectangular board around an axis running diagonally through sounds like it's not the simplest solution.

My question is: since w has x and y components, can I treat Lx and Ly separately and combine wx and wy afterwards? I'm guessing so, as L is a vector, but I've never done this before. Also, is there a trick similar to the parallel axes theorem to calculate I when you rotate the axis around the center of mass? Thanks!

 

[kuruman]

Hi Raphael30 and welcome to PF.

How do you mean ω has x and y components? Can you provide a drawing and include the axes? I assume gravity is acting on the system, correct?

If you choose to calculate angular momentum about the CM of the ball + plank system, then yes, you have to use the parallel axis theorem. It's not a trick, it's the correct way to go about it. For that, you need to know, look up or derive the moment of inertia of the plank about its CM.

 

[Raphael30]

Made this beautiful paint drawing.

The pink line is where I suppose the resulting instantaneous axis of rotation should be, which is why I said ω has x and y components. Since gravity and tension are both on the same plane as the axis of rotation at this instant (and I only have to calculate ω at the time of the collision), I supposed there was no external torque and angular momentum was conserved. The mass of the ball is only 20g next to 900g for the plank, meaning the parallel axis theorem hardly changes the moment of inertia, but the angle of the axis of rotation and the rectangular shape still makes it annoying to integrate. I'm pretty sure I can use L=Iω to calculate ω, my question is really whether it would work to use the x distance between the ball and the center of mass to calculate L around a vertical axis and find ω_y, then do the same for ω_x and combine them with ω^2 = ω_y^2 + ω_x^2

 

[RPinPA]

Those are not very convenient x and y axes for the reasons you describe. I would define coordinate axes parallel and perpendicular to that diagonal and divide the rectangle into strips parallel to the axis. Let's say x is perpendicular to the diagonal and y is parallel, so you're dividing the rectangle into strips dx which all have the same distance from the axis.

It's not hard to work out what the limits of x (perpendicular distance from the diagonal) are or what the length of a strip is at a given value of x, and thus the value of mr^2 for such a strip. Then integrate that over dx.

 

[haruspex]

The pink line is where I suppose the resulting instantaneous axis of rotation should be

It won't be. The plate will acquire some net linear motion.

my question is really whether it would work to use the x distance between the ball and the center of mass to calculate L around a vertical axis and find ω_y, then do the same for ω_x and combine them with ω^2 = ω_y^2 + ω_x^2

Yes, that is definitely the way to go.

 

[Raphael30]

Thanks! I have one final question: in this case, how does the collision affect the tension in both ropes immediately after? The added mass of the ball should increase the tension in the right rope, but is there another factor when the plate is still straight? I was thinking maybe the centripetal acceleration of the plate could affect the tension? Especially on the left end, the rotation implies the end of the rope has fairly strong acceleration and, while the acceleration is neutral over the entire plate, it is more downwards on the left side and upwards on the right end. It doesn't really make sense how a tension that generates no torque would affect the rotation anyway, but I'm really unsure about this. Thanks in advance if anyone can explain this to me.

 

[haruspex]

maybe the centripetal acceleration of the plate could affect the tension?

Quite so.
You can find the velocity at each of the top two corners just after the impact. That gives you the centripetal accelerations of those two points, and thus a linear and rotational acceleration of the plate (+ball). From that you should be able to determine the additional tensions.