klarge
- 5
- 0
1. Problem: Use the spiral r = 5(e^.1θ). Find the area of the region in Quadrant I that is outside the second revolution of the spiral and inside the third revolution.
2. Homework Equations :
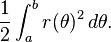
3. Attempt at solution:
My problem with finding the area of a polar graph is determining the bounds, so to get the right bounds for this graph do I set the equation equal to zero? I am really at a loss as to how to set up the bounds. Any hints would be helpful.
2. Homework Equations :
3. Attempt at solution:
My problem with finding the area of a polar graph is determining the bounds, so to get the right bounds for this graph do I set the equation equal to zero? I am really at a loss as to how to set up the bounds. Any hints would be helpful.