Calculating c in Schroedinger Equations

[rayfieca]

Homework Statement

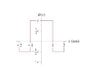
I have attached a graph of a Psi^2 versus position (x) graph. The question asks me to calculate the constant c in nm^(-1/2)

Homework Equations

¡¹h2 d2Ã(x) dx2 + U(x)Ã(x) = EÃ(x)
Also, I know that you have to use normalization so that The integral of cPsi^2=1.

The Attempt at a Solution

I am just not sure how to come up with an integral for the graph. Also, is there a general procedure for calculating these constants so that I can reproduce it in other problems?

 

[rayfieca]

Actually it is a Psi(x) versus x graph not Psi^2. My apologies.