Calculating Capacitor Ripple Voltage: Ideal vs ESR of 0.2 Ohms

[Xyius]

Homework Statement

This homework problem is for my power electronics course I am currently taking.

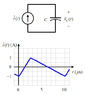
The network shown to the right (SEE ATTACHED IMAGE) is used to
study the output voltage ripple of particular
types of dc-to-dc converters. Note that \tilde{i}(t)
and \tilde{v}_C(t) represent ripple quantities that
have zero average value – they are not
phasors. Sketch the capacitor ripple voltage,
assuming the capacitor is 10 \muF and is …
a. ideal.
b. has an ESR of 0.2 Ohms

Homework Equations

Equation 1:
i(t)=C\frac{d}{dt}v(t)

Equation 2:
ESR=R_{lead}+\frac{1}{R_{leakage}(\omega C)^2}

The Attempt at a Solution

So for part A, I believe all I do is solve Equation 1 for voltage above by integration of a piecewise function that defines the current i(t). Not so bad.

Part B is what is confusing me. If the capacitor now has an associated resistance with it, it can essentially be modeled as a capacitor and resistor in series. To me this means that an impedance with a real and imaginary part is created. But this is confusing because the problem says they are not phasors, and this is apparent by what the solution will be for the voltage for part A (a piecewise function made up of quadratic expressions). I am not sure how to incorporate this resistance in what the ripple voltage will look like.

 

[rude man]

In part (a), Vc = (1/C)integral of i dt.
What is the corresponding expression for part (b) for which ESR = R?

 

[Xyius]

That is what is confusing me. That equation is derived in the following way.

q(t)=C v(t)
\frac{d}{dt}q(t)=\frac{d}{dt}C v(t)
i(t)=C \frac{d}{dt}v(t)

When now there is a resistance, I am not sure which ones of these quantities changes. My only thought is to say that when there is a series resistance, it adds a voltage drop of i(t)R So the total voltage drop becomes the following.

V=\frac{1}{C}q+IR
\frac{d}{dt}V=\frac{1}{C}\frac{d}{dt}q+\frac{d}{dt}IR
\frac{d}{dt}V=\frac{1}{C}I+\frac{dI}{dt}R

Integrating both sides with respect to t gives the following.

V=\frac{1}{C}\int I dt + IR

Writing it in the problems notation it would be.

\tilde{v}(t)=\frac{1}{C}\int \tilde{i}(t) dt + \tilde{i}(t)RWould this be correct?

 

[rude man]

That is what is confusing me. That equation is derived in the following way.

q(t)=C v(t)
\frac{d}{dt}q(t)=\frac{d}{dt}C v(t)
i(t)=C \frac{d}{dt}v(t)

When now there is a resistance, I am not sure which ones of these quantities changes. My only thought is to say that when there is a series resistance, it adds a voltage drop of i(t)R So the total voltage drop becomes the following.

V=\frac{1}{C}q+IR
\frac{d}{dt}V=\frac{1}{C}\frac{d}{dt}q+\frac{d}{dt}IR
\frac{d}{dt}V=\frac{1}{C}I+\frac{dI}{dt}R

Integrating both sides with respect to t gives the following.

V=\frac{1}{C}\int I dt + IR

Writing it in the problems notation it would be.

\tilde{v}(t)=\frac{1}{C}\int \tilde{i}(t) dt + \tilde{i}(t)RWould this be correct?

Yes.
Since you already have the graph for R=0 it should be very easy to add the IR term, right?

 

[rude man]

Yes. \tilde{v}(t)=\frac{1}{C}\int \tilde{i}(t) dt + \tilde{i}(t)R
Since you already have the graph for R=0 it should be very easy to add the IR term, right?

Remember the area under a complete cycle is zero.

 

[Xyius]

This is what I got (See attached). The top is the ideal case. Seems correct. For the second part, I simply added 0.2 multiplied by the piece-wise functions I got earlier for the current. Was this the correct way to do this?

 

[rude man]

This is what I got (See attached). The top is the ideal case. Seems correct. For the second part, I simply added 0.2 multiplied by the piece-wise functions I got earlier for the current. Was this the correct way to do this?

This may be OK but the areas over and under the curve for one cycle should be the same. That's because the dc (average) content of i(t) = 0 and so the capacitor voltage must also have zero dc component over 1 cycle. And of course so must Ri(t).

In graphing parts (a) and (b) did you have Vc(t=0) = 0? If so, then V(0) = 0 for part (a) and V(0) = -R for part (b).

 

[Xyius]

When I was solving the integral equation I set Vc(t=0) to zero. Hope that was okay.

Thank you for all your help!

 

[rude man]

When I was solving the integral equation I set Vc(t=0) to zero. Hope that was okay.

Thank you for all your help!