supercali
- 53
- 0
[SOLVED] center of mass
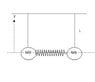
2 bodies m1 and m2 are hanged from the ceiling with a thread with length L. the bodies are also connected to one another with a thread which length is equal to the length from the masses to the hanging point. around that thread there is a spring contracted and its mass can be neglected. the potential eng. of the spring is U. at a certain moment the thread between the mass m1 and m2 is being torn and the spring pushes the masses. what is the hightest height that m1 can go up to relatively to the first place it was
attched a scheme of the problem
i thought of using the concept to center of mass and say that the center went up...but i don't really know how to implement this...
please help if you can
Homework Statement
2 bodies m1 and m2 are hanged from the ceiling with a thread with length L. the bodies are also connected to one another with a thread which length is equal to the length from the masses to the hanging point. around that thread there is a spring contracted and its mass can be neglected. the potential eng. of the spring is U. at a certain moment the thread between the mass m1 and m2 is being torn and the spring pushes the masses. what is the hightest height that m1 can go up to relatively to the first place it was
attched a scheme of the problem
Homework Equations
The Attempt at a Solution
i thought of using the concept to center of mass and say that the center went up...but i don't really know how to implement this...
please help if you can
Attachments
Last edited: