Calculating Change in Energy: A Graph Analysis

[RandiSS]

Homework Statement

A gas expands from I to F in the figure. The energy added to the gas by heat is 486 J when the gas goes from I to F along the diagonal path.

1. What is the change in internal energy of the gas?
Answer in units of J.
2. How much energy must be added to the gas by heat for the indirect path IAF to give the same change in internal energy? Answer in units of J.

Relevant Equations

ΔU = Q + W
W=pΔV

Not a solution. This is the graph provided.

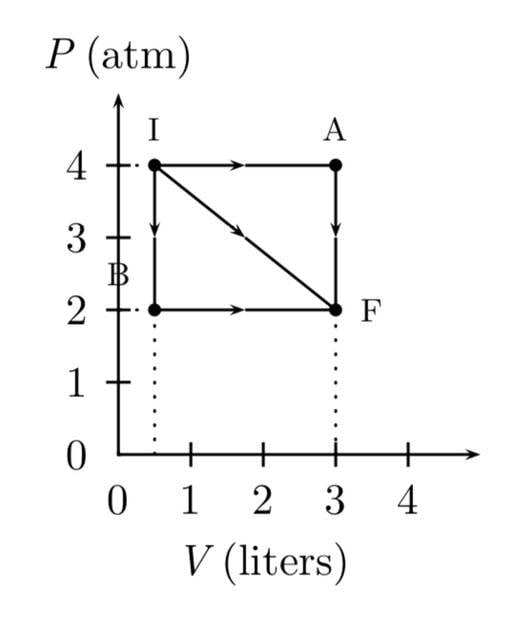
I think I start with finding the magnitude of the IF vector but I’m not sure. And I don’t know where to go from there.

 

[haruspex]

Can you at least calculate the change in internal energy and heat added to go from I to A?

 

[kuruman]

Alternatively, apply the first law for the direct path IF. You are given the heat added Q_IF and you are looking for the change in internal energy ΔU_IF. Can you find W_IF from the graph? Note that your relevant equation should be ΔW=pΔV.

 

[RandiSS]

Alternatively, apply the first law for the direct path IF. You are given the heat added Q_IF and you are looking for the change in internal energy ΔU_IF. Can you find W_IF from the graph? Note that your relevant equation should be ΔW=pΔV.

Hey I got it figured out. Thanks for the help. :)