Calculating Coefficient of u^16v^2 in (u^2 + v)^10 Expansion

[mr_coffee]

Hello everyone. I was wondering if there was a fast way to figure out the following:

THe question is:
What is the cofficient of u^16v^2 in the binomial expansion of (u^2 + v)^10?

Well the answer is 45.

I know what the binomail theorem is:

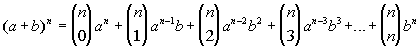
and I can put (u^2 + v)^10 in that form
a = u^2
b = v
n = 10

(10 choose 0)*(u^2)^10 + (10 choose 1)*(u^2)^(9)*v + (10 choose 2)*(u^2)^(8)*v^2...

Okay so i found (10 choose 2) is where the coefficent of the binomial expansion of (u^2 + v)^10. But is this how your supppose to do it? Write it out like that? Or is there a faster way?

I also got 45 by just taking (10 choose 2) = 45.

So my question is, is there another way to compute this? It looks like the professor did somthing like:

(u^16)*v^2 = (u^2)^8*v^2 I see they equal each other but I'm not sure how this is connecting things together and how its figuring out the co-efficent.

ANy help would be great!

 

[chroot]

In your binomial expansion, b = v, and a = u^2.

In the same term, a is raised to the (n-2) power. (u^2)^(10-2) = (u^2)^8 = u^16, so this checks out okay. It's the right coefficient.

The coefficient with b raised to the second power is the one with (n choose 2) in front. The coefficient of this term, (10 choose 2), is 45.

- Warren

 

[mr_coffee]

Thanks Warren, I see your explanation for making sure it checks out but how did u know that the coefficient with b raised to the second power was the correct choice with (n choose 2) without writing it out? Or was that from inspection?

It looks like to find the co-effient you need to recongize 2 things,
#1. That n is whatever binomial expansion he is asking for, in this case 10, from (u^2+v)^10

#2. and look what v is raised too, which is u^16v^2

Then just toss the (10 choose 2) = 45 like you said.

Am i getting that right or did i just make an assumption its always going to work like that?

Like for instance, here is another problem:

What is the coefficient of x^5 in the binomial expansion of (x+2)^8

His answer is 448,

would it be (8 choose 5)? that gives me 56 which isn't right so i guess not, hm.

 

[drpizza]

Something that might help is to see all the coefficients at once a few times. Do a quick search for Pascal's triangle (use google or whatever.) Incidentally, while others are looking at this, can anyone name some realistic applications where you'd only need the coefficient of one of the terms in a binomial expansion?

edit: Ohhh, I see where you had trouble...
Don't forget that not only do get the coefficient from the combination, but when you have x^5, you also have a 2^3. That term is 56x^5 * 8

 

[matt grime]

What is the coefficient of x^5 in the binomial expansion of (x+2)^8

His answer is 448,

would it be (8 choose 5)? that gives me 56 which isn't right so i guess not, hm.

it is x +2 in there. The 2 is important. You can't forget it. You did forget it. The coefficient of x^5y^3 in (x+y)^8 would just be 8 choose 5 (or 8 choose 3 since those are the same), as would the coefficient of x^5 in (1+x)^8