indojo24
- 2
- 0
Homework Statement
I want to ask about a question which is related to dissipation of electric power.
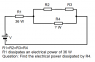
Here's a quick picture of my problem:
R1=R2=R3=R4
R1 dissipates an electrical energy of 36 W
Question: What is the electrical energy dissipated by R4?
Please look at the circuit I've attached below.
This is a Junior High physics questions which I don't understand. Thanks in advance.
Homework Equations
R=V2/P
R=(Ωhm)
P=(Watt)
V=(Volt)
The Attempt at a Solution
I haven't made any attempt because it's confusing.
Possible choices:
a. 18 W
b. 16 W
c. 9 W
d. 4 W