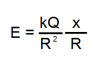You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Calculating Electric Field from a Dipole: Is This Equation Accurate?
- Thread starter novelriver
- Start date
AI Thread Summary
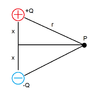
The discussion focuses on the accuracy of the equation used to calculate the electric field at point P from a dipole. It clarifies that the electric field, represented as a vector, requires careful consideration of vector addition from both positive and negative charges. The initial misunderstanding about the components of the electric field is corrected, emphasizing that the x-components cancel while the y-components do not. The final equation derived is E = 2kQx/r^3, indicating the correct approach to calculating the electric field. The conversation highlights the importance of systematic problem-solving and accurate variable naming in physics calculations.
Physics news on Phys.org
BvU
Science Advisor
Homework Helper
- 16,212
- 4,925
Hello Novel, 
You don't want to delete the template; it's very useful for you as well as for us. See the guidelines.
Answer to your question: No. ##\ \vec E\ ## is a vector. What does your E describe, you think ?

You don't want to delete the template; it's very useful for you as well as for us. See the guidelines.
Answer to your question: No. ##\ \vec E\ ## is a vector. What does your E describe, you think ?
novelriver
- 7
- 0
BvU said:Hello Novel,
You don't want to delete the template; it's very useful for you as well as for us. See the guidelines.
Answer to your question: No. ##\ \vec E\ ## is a vector. What does your E describe, you think ?
Thanks for your reply. I'll make sure to not delete the template next time. I think my E describes the magnitude of the electric field. After calculating the magnitude, I can decide if it's positive or negative. So in this case, E is negative, because E is going down, away from positive and toward negative. Is this right?
BvU
Science Advisor
Homework Helper
- 16,212
- 4,925
I'll give you some leeway because you are new here (let's hope I don't get chastized for that).
Also because I think you have a fair idea what you are doing, but you stumble because you are going too fast.
Again, ##\vec E## is a vector. I've drawn the two contributions from the +Q and the -Q in the figure.
There are no other contributions, so the field at P is the sum of these two. The vector sum, that is. Your job to do this vector addition. Andf yes, x/r appears in there (not x/R but x/r; I don't see or know of R in your post. Work accurately ). And yes, it's downwards. Easy exercise, but a good vehicle to learn to work systematically.
). And yes, it's downwards. Easy exercise, but a good vehicle to learn to work systematically.
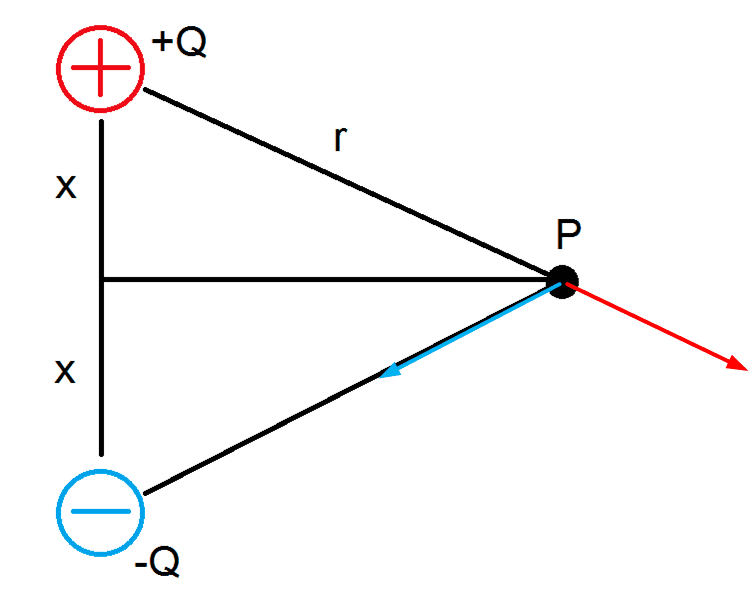
Also because I think you have a fair idea what you are doing, but you stumble because you are going too fast.
Again, ##\vec E## is a vector. I've drawn the two contributions from the +Q and the -Q in the figure.
There are no other contributions, so the field at P is the sum of these two. The vector sum, that is. Your job to do this vector addition. Andf yes, x/r appears in there (not x/R but x/r; I don't see or know of R in your post. Work accurately
novelriver
- 7
- 0
BvU said:I'll give you some leeway because you are new here (let's hope I don't get chastized for that).
Also because I think you have a fair idea what you are doing, but you stumble because you are going too fast.
Again, ##\vec E## is a vector. I've drawn the two contributions from the +Q and the -Q in the figure.
There are no other contributions, so the field at P is the sum of these two. The vector sum, that is. Your job to do this vector addition. Andf yes, x/r appears in there (not x/R but x/r; I don't see or know of R in your post. Work accurately). And yes, it's downwards. Easy exercise, but a good vehicle to learn to work systematically.View attachment 105666
I think I understand.
E = kQ/r2 * cos(theta) because the y-components cancel out and we just want to get the x-component. I'll call the horizontal distance d (in a real problem it would be given or I could find it with trig), so cos(theta) = d/r. Therefore E = kQ/r2 * d/r = kQd/r3.
novelriver
- 7
- 0
novelriver said:I think I understand.
E = kQ/r2 * cos(theta) because the y-components cancel out and we just want to get the x-component. I'll call the horizontal distance d (in a real problem it would be given or I could find it with trig), so cos(theta) = d/r. Therefore E = kQ/r2 * d/r = kQd/r3.
I just realized my mistake. It's the x-components that cancel, not the y. So E = kQ/r2 * sin(theta) = kQ/r2 * x/r = kQx/r3 and then multiply by 2 because there are two charges acting on P in the same direction. So E = 2kQx/r3.
BvU
Science Advisor
Homework Helper
- 16,212
- 4,925
Looks good to me. x and y are a bit confusing here because of the x's in the figure.
novelriver
- 7
- 0
BvU said:Looks good to me. x and y are a bit confusing here because of the x's in the figure.
Right, I realized that I should have chose a different variable name than x. Thank you for your help! I appreciate it!
Similar threads
- Replies
- 11
- Views
- 3K
- Replies
- 14
- Views
- 1K
- Replies
- 10
- Views
- 524
- Replies
- 2
- Views
- 2K
- Replies
- 25
- Views
- 3K
- Replies
- 7
- Views
- 2K
- Replies
- 2
- Views
- 661
- Replies
- 19
- Views
- 4K
- Replies
- 1
- Views
- 2K
- Replies
- 4
- Views
- 3K
Hot Threads
-
Torque biomechanics
- Started by Naucus
- Replies: 6
- Introductory Physics Homework Help
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
-
How do you calculate the pull of this piston?
- Started by vdance
- Replies: 27
- Introductory Physics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math