al_famky
- 28
- 0
calculating electric fields due to continuous charge distributions?
a question I came across doing some electric field questions, and the answer was really confusing.
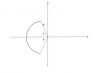
Charge is distributed along a linear semicircular rod with a linear charge density λ as in picture attatched. Calculate the electric field at the origin
for the first question, the magnitude of E was calculated with dE=\frac{adθλ}{4\pi\epsilon_{0}a}, but why is there only one "a" in the denominator, not a^{2}? The final result was this equation \int^{\phi}_{-\phi}\frac{λcosθdθ}{4\pi\epsilon_{0}}=\frac{λsin\phi}{2\pi\epsilon_{0}} which makes sense only if the "a" was dropped.
Thanks to anyone who'd be willing to explain the answers!
a question I came across doing some electric field questions, and the answer was really confusing.
Homework Statement
Charge is distributed along a linear semicircular rod with a linear charge density λ as in picture attatched. Calculate the electric field at the origin
Homework Equations
The Attempt at a Solution
for the first question, the magnitude of E was calculated with dE=\frac{adθλ}{4\pi\epsilon_{0}a}, but why is there only one "a" in the denominator, not a^{2}? The final result was this equation \int^{\phi}_{-\phi}\frac{λcosθdθ}{4\pi\epsilon_{0}}=\frac{λsin\phi}{2\pi\epsilon_{0}} which makes sense only if the "a" was dropped.
Thanks to anyone who'd be willing to explain the answers!
Last edited: