cathb
- 3
- 0
Hi,
I had this question in my homework:
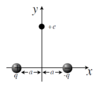
An electric dipole consists of two equal loads and signs opposite separated by one distance which equals 2a. Show how the module of the electric force resulting on a proton (load +e) placed directly on the Y=axis at a very long distance from the dipole (y>>a) is given by Fe = 2aekq/y^3
The usual equation for the electric force is: Fe= keq/r^2
I tried to replace the distance r^2 with Pythagore: a^2 + y^2 = r^2, but i didnt find the y^3
Could anybody help me?
I had this question in my homework:
An electric dipole consists of two equal loads and signs opposite separated by one distance which equals 2a. Show how the module of the electric force resulting on a proton (load +e) placed directly on the Y=axis at a very long distance from the dipole (y>>a) is given by Fe = 2aekq/y^3
The usual equation for the electric force is: Fe= keq/r^2
I tried to replace the distance r^2 with Pythagore: a^2 + y^2 = r^2, but i didnt find the y^3
Could anybody help me?