I like Serena said:
If I understand correctly, you don't know how to convert spherical coordinates (r,ϕ,θ) to cartesian coordinates (x,y,z)?
Well, you are using an extra "r" and you are missing an "y", so that might muddy your set of equations...
The conversion from spherical to cartesian is:
x = ρ sin ϕ cos θ
y = ρ sin ϕ sin θ
z = ρ cos ϕ
where ρ is the Earth radius, ϕ is the colatitude (90° - latitude), and θ is the longitude.
AH HAH! I got so wrapped up in the math that I forgot that this was an actual problem and not an exercise. The term I was missing was the radius of the Earth (ρ). That made all the difference.
Using these definitions (I'm using N and E as positive directions):
SF: θ=33.75°, ϕ=-84.4°
AT: θ=37.78°, ϕ=-122.42°
So now I've converted my terms:
SF = 6.3781e6m <-.8275, -.5529, .0976>
AT = 6.3781e6m <-.6672, -.5171, -.5361>
Looking at my terms, they look real good. I would expect that my vectors from the center of the Earth to any point on the surface would be the radius and if I find the magnitude of my vectors they are 1 (well, out to 4 decimal places, so close enough).
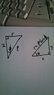
Using a sketch, I've determined that D = SF - AT (image attached)
I found my straight line distance between the two points, which is .7875ρ.
The angle between the two vectors (A.S = ||A|| ||S|| cos θ) is 38.215° or .66698 radians.
The arc length is the angle of the arc * radius (technically θ/total degrees in circle * C) .
s = θ * 6.3791e3 km, I used radians (but to make double sure I also used degrees and got the same value)
But I come out with 4254.050 km. I found a Great Circular Calculator online that say the distance between the two cities is 3443.341 km.
I've made an error somewhere. You mentioned a colatitude and I don't know what that is. I am wondering if the angle measures I'm using are not the correct ones. Could you verify that my triangles are using the correct angle measures or help me to understand my error (image attached)?
OR considering the distances, is this an acceptable amount of error?