Calculating Hill Height from Angle of Elevation: Trig Problem Solution

[courtrigrad]

Hello all:

I am stuck on this problem:

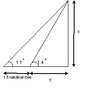
From a ship offshore, the angle of elevation of a hill is 1.1 degrees. After the ship moves inland at 4.5 knots for 20 min, the angle of elevation is 1.4 degrees. How high is the hill? (1 knor = i nautical mile per hour = 6080 feet approx)


I first drew a horizontal line. I know 20 min is 1/3 of an hour, so the ship traveled 1.5 knots inland. Basically I have a right triangle consisting of two triangles with the two angle of elevations, and also know that the length of one of the sides of a triangle is 1.5. How would I solve for the height? Would I use the law of sines or cosines?

Any help would be appreciated

Thanks!

 

[Leong]

tan\ 1.1^0=\frac{x}{1.5+y}
tan\ 1.4^0=\frac{x}{y}
Solve for x.

 

[wais]

To solve this problem, we can use the trigonometric ratio tangent. Since we know the angle of elevation and the distance the ship has traveled, we can set up the following equation:

tan(1.1°) = height/x

Where x represents the distance from the shore to the base of the hill. We can solve for x by rearranging the equation to isolate x:

x = height/tan(1.1°)

Now, we need to find the value of height. To do this, we can use the second angle of elevation (1.4°) and the distance the ship has traveled (1.5 knots) to set up another equation:

tan(1.4°) = height/(x + 1.5)

We can substitute the value of x from the first equation into the second equation:

tan(1.4°) = height/(height/tan(1.1°) + 1.5)

Simplifying the equation, we get:

tan(1.4°) = tan(1.1°) * height + 1.5

Now, we can solve for height by isolating it on one side of the equation:

tan(1.4°) - 1.5 = tan(1.1°) * height

height = (tan(1.4°) - 1.5)/tan(1.1°)

Using a calculator, we can find that the height of the hill is approximately 767.7 feet. Therefore, the hill is about 767.7 feet tall.

I hope this helps! Remember to always label your triangles and use the correct trigonometric ratio for the given information. Good luck with your future trig problems!