ironman
- 17
- 0
Hello (:
Can someone help me calcultating this limit (as x → ∞)
This is the function:
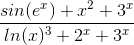
If I just kept deriving sin(e^x) nothing really happened.
So I tried using L'Hopital but partly, i guess:
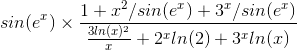
so:
(1 or -1) × 1 + 0 + 0 / 0 + ∞ + ∞The answer must be 1 (according to wolfram alpha) but i don't see how that can be...
Can someone help me calcultating this limit (as x → ∞)
This is the function:
If I just kept deriving sin(e^x) nothing really happened.
So I tried using L'Hopital but partly, i guess:
so:
(1 or -1) × 1 + 0 + 0 / 0 + ∞ + ∞The answer must be 1 (according to wolfram alpha) but i don't see how that can be...