EchoTheCat
- 21
- 1
Homework Statement
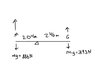
Determine the mass of a 4.5 meter beam, if it is balanced on a fulcrum 2.04 meters from the left end. A 886 N man stands on the very left end, and a 393 N girl stands on the right end. [/B]
Homework Equations
T = Fr
The Attempt at a Solution
The torque applied by the man would be 886 N * 2.04 m = 1807.44 N*m.
Since the length of the beam on the right side is 4.5-2.04 = 2.46 m, the torque applied by the girl is 393 N * 2.46 m = 966.78 N*m.
Since the fulcrum is slightly closer to the left, the torque applied by the beam is (2.46-2.04 m)*9.8*mass of the beam.
Since the torques must cancel, 1807.44 = 966.78 + 4.116*m
m = 204.242 kg Not the right answer though.