Calculating minimum torque and energy in a crane system?

[freshcoast]

1. Problem statement

A simple model of a crane involves a motor driven drum that winds or unwinds a steel cable onto the drum. The cable passes through a pair of guides and over a pulley at the end of the crane arm. Ignore the mass of the cable in your calculations. The drum has a mass of 650kg and a 1.4m radius. The pulley has a radius of 85 cm and a mass of 295kg. The load has a mass of 1800kg.

a) if the load is to be accelerated from rest to a constant lifting speed of 30cm/s over a distance of 10cm, what minimum torque must the motor provide?

b) what minimum amount of energy is required by the motor to lift the load from rest to a final height of 10m where it ends at rest?

c) what are the tensions in the section of cable from the drum to the pulley, and from the pulley to the load as the load is accelerated? What are the tensions when the load is lifted at constant speed?

2. Related equations
Rotation equations
Torque equations
Moment of inertial equation

3. Attempt at solution

For part a) what I did so far is I know there is a linear tangential equation that the load is lifted at a distance of .1m which I solved using Newtons kinematic then I converted that to a rotational acceleration by dividing it by the radius of each of the pulley and the drum. Which gives me two different alphas, I then find the moment of inertia for the drum and the pulley which then I can find the torques for each. So since I found the torques do I just sum those up and it will give me the minimum torque needed? But my question is how do I count for the mass of the load? Or is my answer correct?

Part b) since the load is starting from rest and ends at rest, wouldn't the kinetic energy equal to 0? Meaning that the total work done would just be the change in potential energy of the mass? But my professor was saying that the easiest way to go about this is that there is 3 stages that the box goes through, which is an acceleration stage, a constant speed stage and a deceleration stage, and then I just integrate the torque by the main drum by the 3 arc lengths that the box goes through? I don't know how to go about doing that, and the one last way that I was suggested is find the rotational kinetic energy for the pulley and the drum and sum those up with the potential energy of the load? I don't know which is the correct way of going about this question..

Part c) I know the tension from pulley to the load is the easy part since I'm just summing up the forces in the y direction when there is an acceleration or not , but from the drum to the pulley, do I just apply the summation of the torque ( when being accelerated ) is I(alpha) = torque(motor) - torque(tension) where torque(tension) is equal to Ft*r and just solve for ft since I have found most of the values already.

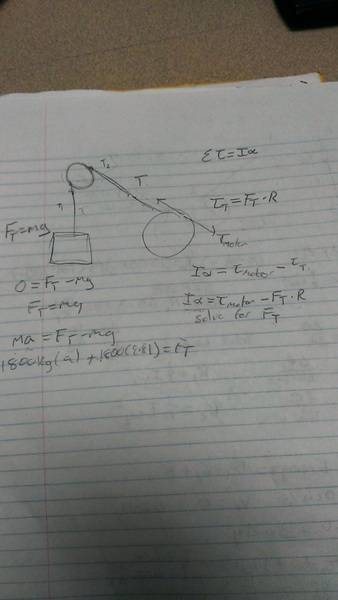Thanks for any input and sorry for the long read!

 

[haruspex]

For part a) what I did so far is I know there is a linear tangential equation that the load is lifted at a distance of .1m which I solved using Newtons kinematic then I converted that to a rotational acceleration by dividing it by the radius of each of the pulley and the drum. Which gives me two different alphas, I then find the moment of inertia for the drum and the pulley which then I can find the torques for each. So since I found the torques do I just sum those up and it will give me the minimum torque needed? But my question is how do I count for the mass of the load?

Try answering this first: if the pulley and drum had zero mass, how would you calculate the torque need to accelerate the load?
The torque needed at the drum to accelerate the drum is easy - you've done that.
The torque needed to accelerate the pulley is a little more subtle. Remember that the drum doesn't 'know' anything about the pulley. All it knows is the tension it has to generate in the cable. So the torque needed at the drum to accelerate the pulley may be different from the torque needed at the pulley itself.
One way to make this all very clear and straightforward is to introduce unknowns for the tensions (different ones for load to pulley and pulley to cable) and do the usual free body analysis on each of the three.

 

[freshcoast]

First of all at this part

One way to make this all very clear and straightforward is to introduce unknowns for the tensions (different ones for load to pulley and pulley to cable)

did you mean from load to pulley and pulley to drum correct?

So what I did is I drew a free body diagram for the load, the pulley and the drum.

for the summation of torques at the pulley it had two different tensions, I labeled T1 as the tension from the load, and T2 is the tension from the drum, which looked like

Ʃ\taupulley = Ipulley\alphapulley
T1Rp + T2Rp = Ipulley\alphapulley

(Rp = radius of pulley)

both tensions are positive because both are rotating in the clockwise which I labeled as the positive direction. Then I did some algebraic maneuver to isolate T2 by itself.

Then I drew a summation of forces for the drum, I'm thinking since there is a force needed to rotate the drum in the clockwise direction in order to pull the load(which I think is the torque that I am looking for), would that mean that there is a T2 pulling the drum to turn in the counter clockwise direction (or negative direction).. so that gives me

(Rd = radius of drum)

Ʃ\taudrum = Idrum\alphadrum
FRd - T2Rd = Idrum\alphadrum

and then I just do some substitution and move around some terms and solve for the F? or maybe that FRd term is just an unknown \tau term that I just solve for?

 

[haruspex]

did you mean from load to pulley and pulley to drum correct?

Ah, yes.

Ʃ\taudrum = Idrum\alphadrum
FRd - T2Rd = Idrum\alphadrum

If FRd is the torque you're trying to calculate, yes.

 

[freshcoast]

I think I made a mistake in one calculation of the pulley, the tension from the load is opposite of the tension by the drum meaning they would be different in signs correct? this is my work I have so far..

which I think seems right

 

[freshcoast]

ok for part B, I'm thinking since my professor suggested using integration,

Could I use the torque that I just found, integrate that to the correct bounds of dθ and to find that is since I have the arc length S which is 10m and R = 1.4m, I use the equation

S = Rθ

solve for θ

then integrate

S \tau dθ

and my bounds would be from 0 to the θ that I found?

 

[haruspex]

T1 is not equal to mg. The load accelerates too. Once you've corrected that you will get the right answer, but by sticking with symbolic algebra a bit longer there's a numerically simpler way. If the cable's acceleration is a, and it runs over a uniform cylinder radius r, then the angular acceleration is a/r, the MI is mr²/2, the torque is amr/2, and the difference in cable tension needed to generate that torque is (amr/2)/r = am/2. So it turns out that the pulley's radius is not relevant.

 

[freshcoast]

I see, I just adjusted the T1 = mg + ma with the tangential a I found because it seemed simpler to me, haha. is my theory for part b correct though?

 

[haruspex]

is my theory for part b correct though?

Since there are no frictional losses or inelastic impulses, and all the energy invested in accelerating the cylinders and load can be recouped by letting their inertia contribute to the final portion of the lift, yes - just consider change in PE of the load.

 

[freshcoast]

That's what I thought at first, but this is my conversation that I had with my professor.

For question 4 part b, if I'm understanding the problem correctly, if the load starts from rest and ends at rest, wouldn't that mean there is no change in kinetic energy, meaning that If I apply the work done by non conservative forces plus initial energy equal to the final energy, the total work done would just equal the final potential energy?

and his reply is

Load starting and ending at rest does indeed mean no NET Work done. However, the best way to do it is to integrate the drum torque over the appropriate limits.

Since S = R theta, you can solve for theta since you know S and R.

I was thinking the change in potential energy would be the easiest way to go about it but I don't know if it is correct since he is suggesting this other way? are both solutions correct? because I'm getting two different numbers for the total energy..

 

[haruspex]

I'm getting two different numbers for the total energy..

If doing it the prof's way gives you a different answer, please post your working.

 

[freshcoast]

sure,

if the minimum torque I calculated in part a is correct, I used the equation

w = ∫\taudθ

where θ = S/R

S = 10, R = 1.4m

\tau = 26127.4 Nm

so when I integrate that, I get, W = 26127.4Nm (7.14) = 186549 Nm or J

whilst the change in potential energy would just be mgh = (1800kg)(9.8m/s^2)(10m) = 176400 Nm or J

 

[haruspex]

if the minimum torque I calculated in part a is correct, I used the equation
w = ∫\taudθ
where θ = S/R
S = 10, R = 1.4m

You seem to be assuming the same torque is maintained for the whole lift of 10m. That won't bring the load to rest at 10m, and it certainly is not the minimum. After reaching the speed required for part a, you can reduce the torque. You can even make it a bit less than that required to keep the load moving at constant speed, since the inertia in the load and cylinders will help. The essential point is that if you only supply enough energy to get the load up 10m and the whole system is then at rest, you must have only put in enough to cover the PE change. There is no KE left in the system, and there are no losses anywhere.
I should just note that using potential energy alone wasn't necessarily going to give the right answer. It might have been the case that the energy invested in part a was already more than that, and the load was doomed to overshoot the 10m mark (in which case, that energy would have been the answer). But it's pretty clear that this is not the case here.