kachi
- 9
- 0
Hello,
My knowledge on fluid mechanics is on a introductory level. When explaining, it would be great if you could explain in simple English and also like teaching to a student who isn't very good at the subject area!
I've been reading a lecture slide and have been trying to follow the example to solve my given problem. I don't really understand how the lecturer got certain parts of the solution though (equation hasn't been explained/defined on any of the slides). I don't understand how the lecturer found the diameter or the suitable velocity is for half-flow.
EDIT: The question doesn't require me to find whether the calculated velocity is suitable, but I would like to know how you do find it.
I have attached the slide that I'm using as an example below.
I used A = pi*D^2/8 and P = pi*D/2 as my problem is for half flow condition.
What is wrong? How do I do this correctly?
Thank you for reading. Any help would be appreciated, thank you.
If water flows from Point D at Kinglake to Point E at Sugarloaf in a lined circular channel laid on a slope of 0.001. If Manning’s n = 0.013 and if the design discharge is 0.07 m^3/s, what diameter channel should be designed for a half-flow condition? What will be the mean velocity in the channel for this condition?
Manning’s n = 0.013
Slope = 0.001
Q, Discharge = 0.03m^3/s
Find diameter of channel for half flow condition.
Find mean velocity of channel in half flow condition.
Mannings equation:[/B]
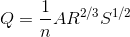
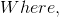
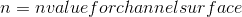
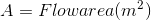
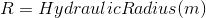
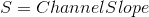
Velocity equation:
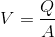
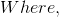
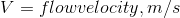
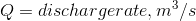
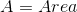
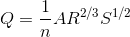
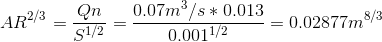
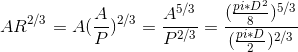
A = pi*D^2/8 and P = pi*D/2
Diamter, D = 0.53m^(8/3)
How do I find the diameter required for the channel from this? Is this (above) the diameter? I don't understand on the attachment below, how 0.52m^(8/3) becomes a diameter of 1.21 metres?
------
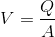
V = 0.07m^3/s/((pi*(0.53)^2)/8) = 0.634 m/s
How do I find whether the velocity I calculated is suitable?
My knowledge on fluid mechanics is on a introductory level. When explaining, it would be great if you could explain in simple English and also like teaching to a student who isn't very good at the subject area!
I've been reading a lecture slide and have been trying to follow the example to solve my given problem. I don't really understand how the lecturer got certain parts of the solution though (equation hasn't been explained/defined on any of the slides). I don't understand how the lecturer found the diameter or the suitable velocity is for half-flow.
EDIT: The question doesn't require me to find whether the calculated velocity is suitable, but I would like to know how you do find it.
I have attached the slide that I'm using as an example below.
I used A = pi*D^2/8 and P = pi*D/2 as my problem is for half flow condition.
What is wrong? How do I do this correctly?
Thank you for reading. Any help would be appreciated, thank you.
Homework Statement
If water flows from Point D at Kinglake to Point E at Sugarloaf in a lined circular channel laid on a slope of 0.001. If Manning’s n = 0.013 and if the design discharge is 0.07 m^3/s, what diameter channel should be designed for a half-flow condition? What will be the mean velocity in the channel for this condition?
Manning’s n = 0.013
Slope = 0.001
Q, Discharge = 0.03m^3/s
Find diameter of channel for half flow condition.
Find mean velocity of channel in half flow condition.
Homework Equations
Mannings equation:[/B]
Velocity equation:
The Attempt at a Solution
A = pi*D^2/8 and P = pi*D/2
Diamter, D = 0.53m^(8/3)
How do I find the diameter required for the channel from this? Is this (above) the diameter? I don't understand on the attachment below, how 0.52m^(8/3) becomes a diameter of 1.21 metres?
------
V = 0.07m^3/s/((pi*(0.53)^2)/8) = 0.634 m/s
How do I find whether the velocity I calculated is suitable?
Attachments
Last edited by a moderator:
