Linus Pauling
- 187
- 0
1. The 10 ohm resistor in the figure is dissipating 40W of power. How much power is the 5ohm resistor dissipating?
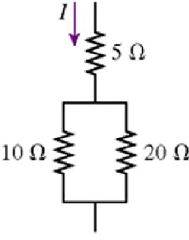
2. P = I2*R
3. I = sqrt(P/R) = 2. I then did P = I2R = (4)(5) = 20 which is incorrect.
2. P = I2*R
3. I = sqrt(P/R) = 2. I then did P = I2R = (4)(5) = 20 which is incorrect.