Calculating pressure to raise a submarine

[inkymadness]

ok a model submarine, so not as exciting as the title suggests! This is a pretty basic physics question so forgive me, I'm just trying to clarify in my own head the increase in water displacement with a decrease in gas pressure. Basically as shown in the diagram below I have a model of the Kursk, basically a metal cube with a mass of 0.128kg, and let's say a density of 2 (haven't decided on material yet). So to give it buoyancy I have to get its density to less than 1 (water thereabouts) and so am going to pump atmospheric air through a 10mm tube at the bottom of the container which will bubble up to a fabric umbrella and increase the volume of the model to raise it. What I need help with is to work out the volume of gas needed to fill the umbrella to get it to raise, the pressure required to pump the gas through the diameter tube at the bottom of the tank, and finally a couple of variance on the mechanism to pump the air and your opinions on whether they'd work. So here's the equations I'm working on and the diagram:

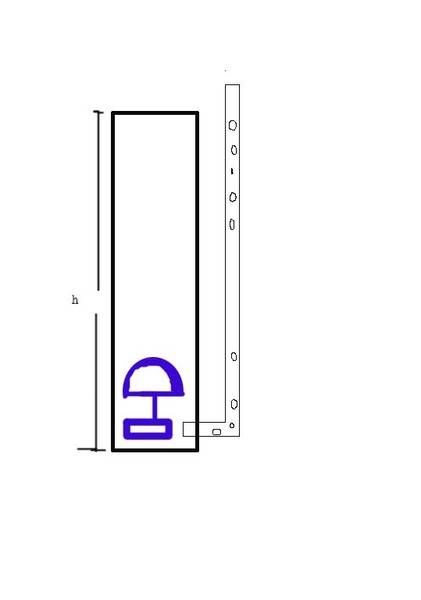
1. Volume of Kursk, 0.04m sided cube = 0.064m3. Density = 2 therefore mass = 0.128kg.
equation to get increase volume to 1< (just use density of 1) P=m/Vgh
h= 2m of water therefore
V = 1/gh/m
V= 0.429m3, so I need to add 0.365m3 of air to get it to raise. Sound right? This is what the volume of the air is in the tube that feeds the container yeah? Will this tube be at 1 atmosphere of pressure regardless of how great the h of the tube is?
2. How do I calculate the pressure needed at the opening of the tube to push the air out of the tube and into the water? I'm thinking P=F/A where A is the area of the tube opening, and the Force is the mass of a 10mm circular water column x gravity x height (F=mgh). Is this correct?
3. I'm thinking of placing a weight into the tube that is greater than the mass required to push the air into the water will this work, and what sort of mass are we talking - I assume once I have the pressure required I can use the equation P=m/Vgh to work out the mass? Thanks muchly in advance and apologise if this is too long a post for such a simple problem, I'm just trying to make it easy for you to understand what I'm talking about. Cheers.

 

[256bits]

This is what the volume of the air is in the tube that feeds the container yeah? Will this tube be at 1 atmosphere of pressure regardless of how great the h of the tube is?

the pressure of water at at depth h is what the air will see as it tries to exit the tube.

 

[MrNerd]

In order to pump the air into the tank, the pressure from the pump must exceed the pressure from the water. If you want a truly accurate answer, you may need some basic calculus as the pressure from the water at different levels of height in the umbrella will change slightly. It won't be much, but it would be slightly more accurate. With your idea of using a weight to push the water down, it seems like it could work. Pressure is indeed equal to F/A, so you should be able to find a mass that can do this. I would first find the pressure using P = ρgh, then use it to find the force necessary by setting it equal to the F/A. Simply solve for F, and you should be able to get the mass necessary in Newtons.