Calculating Probabilities using Distribution Function F

[mathmari]

Hello...!I need some help...!
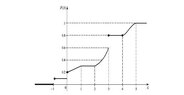
Let the distribution function F of a random variable X given in the following attachment. Calculate the following:
P(X=-1), P(X<0), P(X<=0), P(X=1), P(X>5), P(X>=5), P(3<=X<=4).

I think that these are the answers:P(X<0)=F(0-)=0.1, P(X<=0)=F(0)=0.2, P(3<=X<=4)=F(4)-F(3)=0.8-0.8=0, P(X>5)=P(X>=5)=0, P(X=-1)=F(-1+)-F(-1-)=0.1-0=0.1, P(X=1)=F(1+)-F(1-)=0.3-0.3=0,but I am not sure...
I hope you can help me...!

 

[Jameson]

Hi mathmari,

Welcome to MHB! I will try to answer the parts I can, although there are a couple of parts where I'm not quite sure about the answer.

a) $P(X<0)=F(0-)=0.1$ This looks good to me.
b) $P(X \le 0)=F(0)=0.2$ (Yes)

c) $P(3 \le X \le 4)=F(4)-F(3)=0.8-0.8=0$ This one I'm not sure about. The reason why is because usually the bottom boundary is not included. I believe that $P(3< X \le 4)=F(4)-F(3)=0.8-0.8=0$ but I'm not sure about how including 3 affects this. Just something to think about.

d) $P(X>5)=P(X \ge 5)=0$ These mustn't always be equal but in this problem I agree. Looks ok to me.
e) $P(X=-1)=F(-1+)-F(-1-)=0.1-0=0.1$ I would write it as $P(X=1)=P(X \le 1) - P(X <1)$ but yep, the final answer looks good.

f) $P(X=1)=F(1+)-F(1-)=0.3-0.3=0$. Again, $P(X=1)=P(X \le 1)-P(X<1)$. The tricky thing here is that for $X \in [0,1]$ the CDF appears to show that $X$ is continuous, not discrete so it seems like an integral might be needed. Not sure on this one, but that's my comment.

Sorry I couldn't completely help you but hopefully this is a start and someone else can comment as well! Once again, welcome to MHB.

 

[mathmari]

Thank you! :)