Calculating Radius & Max Speed of Rock in Figure D

[huskydc]

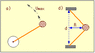
as shown: in the picture, look at figure d) (attachment) don't worry about figure a) --- given:

720 gm rock

each string has a tension of 29 N

the rock is held by two of the 45 cm strings with ends 56 cm apart and whirled in a circle between them. Neglect gravity.
What is the radius of the circle of motion?


what is the maximum speed the rock can have before the string breaks?

 

[Pyrrhus]

Hmm, this is a curvilinear trajectory dealing with only normal acceleration component (radial), apply Newton's 2nd Law. Now that i think about it you can calculate the radius through trigonometry . If you have any more questions i will come back later today, after a good night sleep.

 

[huskydc]

well, i found the radius to be 35.22 cm. and i also found the respective angle between direction of acceleration and the string tensions. from each string to the r as shown, angle is 38.48 degrees. but i don't know where to go from here

 

[Pyrrhus]

Yes now you need to apply Newton's 2nd Law

Now with \theta

T \cos \theta + T \cos \theta = m \frac{v^2}{R}

solve for v.

 

[huskydc]

didn't work cyclovenom,

but how did you come up with that equation?

 

[Pyrrhus]

It should have worked, well the Tension have 2 components, one of them is acting radially, and because there are two tensions both of them hace 1 component acting as the centripetal force. Rememeber to convert the mass of the rock to kilograms!.

 

[Päällikkö]

didn't work cyclovenom,

but how did you come up with that equation?

Horizontal components of T:
T_x = Tcos\theta, where \theta = sin^{-1}(\frac{d}{2s}), where d = 0,56m and s = 0,45m

So, the equation solves into:
v = \sqrt{\frac{2Tcos(sin^{-1}(\frac{d}{2s}))\sqrt{s^2-(\frac{d}{2})^2}}{m}}


In my markings sin^{-1} = arcsin