skybox
- 37
- 0
Hi all, I am having an issue trying to solve the following problem
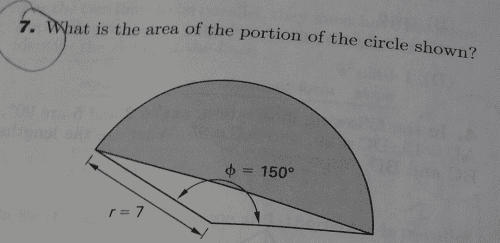
I know that the radius of the circle is 7 and the angle of the segment is 150°
Area of a circle: A = \pi{r}^2
Area of the sector of the circle: A = \frac{n}{360}\pi r^{2}
Area of a triangle: A = \frac{n}{360}\pi r^{2}
I know to get the final solution to get the area of that particular part of the circle, I need to subtract the whole area of the circle with the segment of the circle (the triangular portion).
To get the area of the triangle portion, I subtract the area of the sector of the circle with the area of the triangle of that portion multiplied by 2 (since there are essentially two triangles). Also, to get the area of the triangular portion, I can use the 30-60-90 rule. To get this:
Short leg:
A_s = \frac{1}{2}H = \frac{1}{2}*7 = \frac{7}{2}
Long leg:
A_l=\frac{1}{2}H\sqrt{3} = \frac{7}{2}\sqrt{3}
Area of whole triangle:
A_t=\frac{1}{2}*\frac{7}{2}*\frac{7}{2}\sqrt{3}*2=\frac{49}{4}\sqrt{3}
Now the area of the whole sector is:
A_t = \frac{150}{360}49\pi-\frac{49}{4}\sqrt{3}
To get the area of just that portion of the circle the question is asking, subtract the area of the whole circle with the answer from above:
A = 49\pi-(\frac{150}{360}49\pi-\frac{49}{4}\sqrt{3})
I was wondering if I am doing this problem correctly? I am not getting any of the answers in the possible solutions. Thanks!
Homework Statement
I know that the radius of the circle is 7 and the angle of the segment is 150°
Homework Equations
Area of a circle: A = \pi{r}^2
Area of the sector of the circle: A = \frac{n}{360}\pi r^{2}
Area of a triangle: A = \frac{n}{360}\pi r^{2}
The Attempt at a Solution
I know to get the final solution to get the area of that particular part of the circle, I need to subtract the whole area of the circle with the segment of the circle (the triangular portion).
To get the area of the triangle portion, I subtract the area of the sector of the circle with the area of the triangle of that portion multiplied by 2 (since there are essentially two triangles). Also, to get the area of the triangular portion, I can use the 30-60-90 rule. To get this:
Short leg:
A_s = \frac{1}{2}H = \frac{1}{2}*7 = \frac{7}{2}
Long leg:
A_l=\frac{1}{2}H\sqrt{3} = \frac{7}{2}\sqrt{3}
Area of whole triangle:
A_t=\frac{1}{2}*\frac{7}{2}*\frac{7}{2}\sqrt{3}*2=\frac{49}{4}\sqrt{3}
Now the area of the whole sector is:
A_t = \frac{150}{360}49\pi-\frac{49}{4}\sqrt{3}
To get the area of just that portion of the circle the question is asking, subtract the area of the whole circle with the answer from above:
A = 49\pi-(\frac{150}{360}49\pi-\frac{49}{4}\sqrt{3})
I was wondering if I am doing this problem correctly? I am not getting any of the answers in the possible solutions. Thanks!