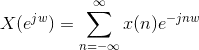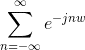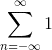Discussion Overview
The discussion revolves around the calculation of the Discrete-Time Fourier Transform (DTFT) of the constant function 1. Participants explore the implications of different values of the frequency variable ω, particularly focusing on cases where ω equals 0 and other multiples of 2π, as well as the behavior of the series involved in the DTFT calculation.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant questions whether the DTFT diverges for ω=1 and seeks clarification on how to calculate the sum for other values of ω.
- Another participant provides a breakdown of the DTFT formula and notes that the sum converges to a geometric series under certain conditions, but diverges for specific values of ω, particularly ω=0.
- A different participant claims to have derived a formula for the DTFT of 1, suggesting that it equals 2π for ω=0 and other multiples of 2π, while asserting it converges to 0 for other values of ω.
- There is a correction regarding the interpretation of the result at ω=0, clarifying that it is not simply 2π but rather involves the Dirac delta function, which is infinite or not well-defined at that point.
- Further discussion includes the use of the inverse DTFT to derive constants related to the Dirac delta function and the periodicity of the DTFT.
- A participant expresses confusion regarding the distinction between the Dirac delta function and the Kronecker delta, seeking clarification on notation and definitions.
- Another participant confirms that the delta function in this context is indeed the Dirac delta and discusses the potential for confusion in notation.
Areas of Agreement / Disagreement
Participants express differing views on the convergence of the DTFT for various values of ω, particularly at ω=0 and other multiples of 2π. There is no consensus on the interpretation of the results, especially regarding the nature of divergence and the role of the Dirac delta function.
Contextual Notes
Limitations in the discussion include unresolved mathematical steps related to the convergence of the series and the definitions of the delta functions. The discussion also highlights the potential for confusion in notation and terminology used in different texts.
Who May Find This Useful
This discussion may be useful for students and practitioners in signal processing, particularly those interested in Fourier analysis and the properties of the DTFT.