Peirianeg
- 8
- 0
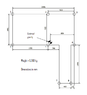
The attachment provided shows a frame in which a large fan is to be rested on. The fan has a weight of 6,060 kg and the location of the centre of gravity is shown in the attachment. I would like to know how to calculate the loads at each point. Could anyone please provide some help on this problem?