Weight Distribution Across Multiple Points

[IanPibworth]

TL;DR Summary

How to calculate reaction forces at multiple points.

Thanks in advance to anyone that can help me solve this problem, its causing me a real headache.

I need to transport a rather large frame that supports a large heavy item. The weight is not evenly distributed along its length. I know the various distances between the supports, the total weight and the center of mass.

I know how to calculate a simple 2 support situation.
Where Wr is weight at rear, Cg is distance from front support to Center of mass and D is distance between the 2 supports. Wf is weight at front.

Wr = (WxCg)/D
Wf = W-Wr

BUT... how do I go about calculating the reaction force (weight on each point) for the problem outlined below??

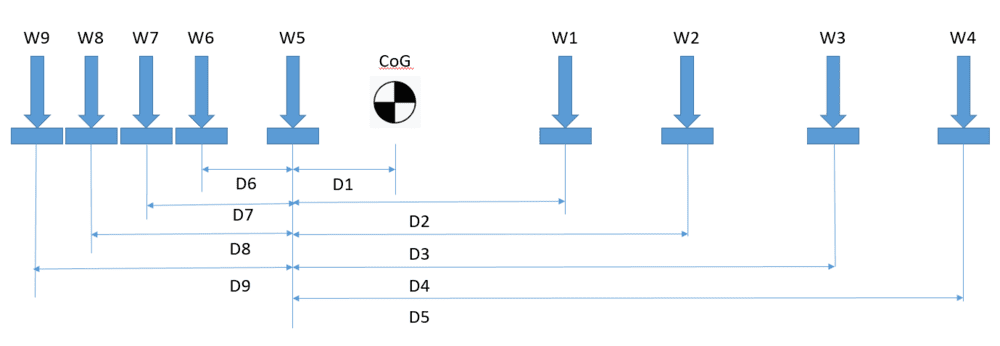
distances

 

[mitochan]

Hello.

Summary: How to calculate reaction forces at multiple points.

Where Wr is weight at rear, Cg is distance from front support to Center of mass and D is distance between the 2 supports. Wf is weight at front.

Wr = (WxCg)/D
Wf = W-Wr

The first equation is rewritten with help of the second,
$$W_r(C_g-D)+W_fC_g=0$$

We can interpret this that summation of weight multiplied by distance from center of gravity, with plus or minus signature according to right or left position of support, is zero.

We can generalize this to multiple weight case, i.e.

$$\sum_i W_i d_i=0$$
$$\sum_i W_i =W$$

where $W_i$ is i-th weight an $d_i$ is its plus or minus distance from Center of Gravity.

 

[jrmichler]

You need to consider the effect of uneven ground/road surface. Start by imagining two cases:
Case 1: Perfectly rigid frame. In that case, the entire load will be supported at exactly two points (ignoring the effect of width at this time. Those two points will change as the road surface changes. Think of cresting a hill vs centered on a valley.

Case 2: A perfectly flexible frame. In that case, the frame will flex with the road, and the load distribution will not change as the road surface changes.

Neither of those cases is a real world case. The real world case is a frame that flexes somewhat, and the local loads increase at the high points of the road and decrease at the low points of the road. This also is the case in the transverse direction where the road can twist the frame. An extreme example is shown below:

I assume the frame is supported by a spring suspension and pneumatic tires. The total stiffness of the frame, spring, and tire assembly is calculated. Then look at the absolute worst case road it will travel over, and calculate the load at each wheel. All this assumes that the load is supported on the frame such that the frame can flex and twist without exerting forces on the load. If the load is some sort of structure tied to the frame at multiple points, then the stiffness of the load must be added to the stiffness of the frame, suspension, and tires. The last step in the calculation is to calculation the forces on the load, and compare to allowable forces on the load. This problem is statically indeterminate, and is analyzed using the methods for statically indeterminate systems.

You need to check the forces of each wheel against the road to make sure you don't break off a wheel, and the local forces on the load to make sure you don't damage the load. There is a section in your Mechanics of Materials book about statically indeterminate system. You will need to spend some time studying that material.
You did keep your textbook, didn't you? If not, buy another copy because you will be using it in the future.

 

[IanPibworth]

Hello.The first equation is rewritten with help of the second,
$$W_r(C_g-D)+W_fC_g=0$$

We can interpret this that summation of weight multiplied by distance from center of gravity, with plus or minus signature according to right or left position of support, is zero.

We can generalize this to multiple weight case, i.e.

$$\sum_i W_i d_i=0$$
$$\sum_i W_i =W$$

where $W_i$ is i-th weight an $d_i$ is its plus or minus distance from Center of Gravity.

I think I understand the logic but struggling to put it into practice. Could you please solve an example using the following numbers so I can fully understand?

All distances are from load point to CoG. + is to the right of CoG and - is to the left of CoG.

W = 10,000Kg

Point A - D1 = 2m Point D D6 = -0.5m
Point B -D2 = 3m Point E D7 = -1.5m
Point C -D3 = 6m Point F D8 = -3m

 

[mitochan]

Hello. For your case
$$2W_1+3W_2+6W_3-0.5W_6-1.5W_7-3W_8=0$$
$$W_1+W_2+W_3+W_6+W_7+W_8=10000$$
This formula gives any two of Ws when other four Ws are given properly.

To explain this arbitrariness let us see a simpler case of homogeneous beam supported by center and both the ends. The equations are
$$W_1-W_3=0$$
$$W_1+W_2+W_3=W$$

solution is
$$W_1=W_3=aW$$
$$W_2=(1-2a)W$$
where a is parameter we can design within 0<a<1/2.

 

[IanPibworth]

Thank-you for your help mitochan

 

[Ahmed]

Hello. For your case
$$2W_1+3W_2+6W_3-0.5W_6-1.5W_7-3W_8=0$$
$$W_1+W_2+W_3+W_6+W_7+W_8=10000$$
This formula gives any two of Ws when other four Ws are given properly.

To explain this arbitrariness let us see a simpler case of homogeneous beam supported by center and both the ends. The equations are
$$W_1-W_3=0$$
$$W_1+W_2+W_3=W$$

solution is
$$W_1=W_3=aW$$
$$W_2=(1-2a)W$$
where a is parameter we can design within 0<a<1/2.

Hello, Could you please provide a detailed calculation on the multiple points ?