Calculating the Net Charge Enclosed by a Closed Surface

[MissPenguins]

Homework Statement

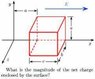
A closed surface with dimensions a = b =
0.294 m and c = 0.3528 m is located as in
the figure. The electric field throughout the
region is nonuniform and given by $\vec{}E$ = ($\alpha$+$\beta$
x²)ˆı where x is in meters, $\alpha$ = 2 N/C, and $\beta$
= 4 N/(Cm²).

See figure in the attachment.

What is the magnitude of the net charge
enclosed by the surface?
Answer in units of C.

Homework Equations

I don't know. I am seriously not lazy.

The Attempt at a Solution

Sorry, I don't know. I really have absolute no clue anything about this problem. I don't really understand the concept either. It would be great if you could explain it and help me out. I promised I did try to do it.
THANK YOU!

 

[I like Serena]

Hi MissPenguins!


The relevant equation is Gauss's law: "The electric flux through any closed surface is proportional to the enclosed electric charge".

Perhaps the wikipedia article http://en.wikipedia.org/wiki/Electric_flux summarizes it in a way you can use?

 

[MissPenguins]

So electric flux = E dot dA?? Can you please explain the concept? Thank you!

 

[vela]

Start by calculating the flux across each face of the cube. Do you know how to do that?

 

[MissPenguins]

Start by calculating the flux across each face of the cube. Do you know how to do that?

Is it calculating the area of the cube? Can you please explain the concept? I am watching a youtube video on electric field now. Thanks.

 

[nayfie]

So electric flux = E dot dA?? Can you please explain the concept? Thank you!

E $\bullet$ dA is a vector dot product. You will need to understand what a dot product is in order to calculate the electric flux.

http://en.wikipedia.org/wiki/Dot_product

 

[vela]

The flux Φ is a measure of how much electric field is crossing a given area. It's given by
$$\Phi = \int \mathbf{E}\cdot d\mathbf{A}$$
where you integrate over the area in question. In this problem, it's easiest to treat each face of the cube separately.

To make use of the definition, you need to understand what's meant by dA and how to calculate the dot product. I suggest you consult your textbook and notes. You'll get a better explanation in your book than we can provide here (plus it'll probably have helpful pictures you won't get here). If you have any specific questions, post those here.

 

[MissPenguins]

Alright, thank you very much. My professor will probably explain it tomorrow. Thanks everyone.