tomtomtom1
- 160
- 8
- Homework Statement
- Stability Of Floating Bodies
- Relevant Equations
- BM = I / V
Hello all
I was hoping someone could help shed some light on understanding an equation for floating bodies.
I am trying to work out the distance between B and M shown in the sketch below:-
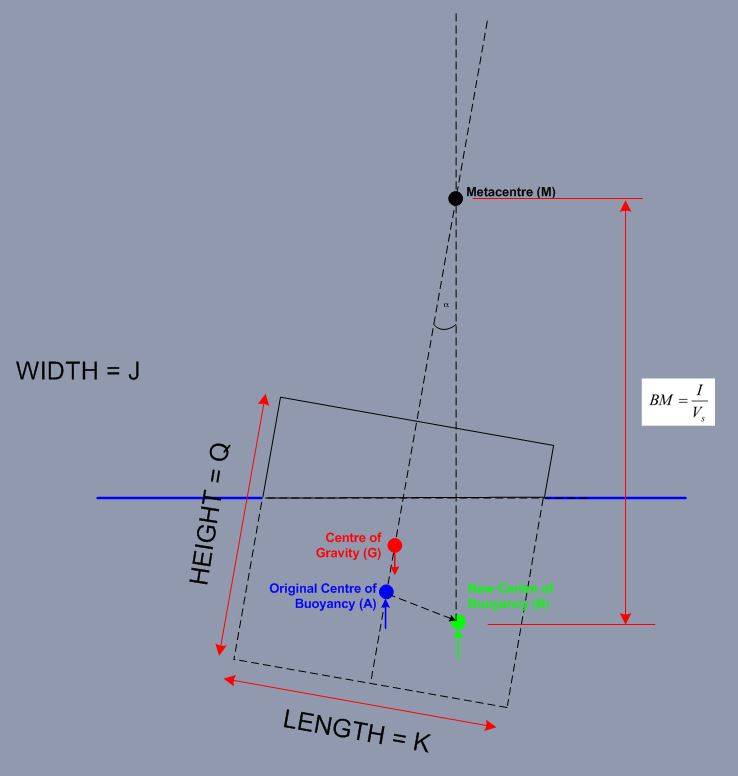
I have been given the equation:-
BM = I/V
BM = is the distance from center of buoyancy to the meta center
I = Is the second moment of area
V = Volume of the submerged portion of the body.
I just want to know how to calculate I?
Is I worked out for the entire floating board or is I worked out for just the portion of the body above the water line or is I calculated to the portion of the body below the water line?
I know that I is bd^3/12 but in my example do i use q for b and k for d - how do you know what values to use and what portion of the bosy I relates to?
Can anyone help?
Thank you.
I was hoping someone could help shed some light on understanding an equation for floating bodies.
I am trying to work out the distance between B and M shown in the sketch below:-
I have been given the equation:-
BM = I/V
BM = is the distance from center of buoyancy to the meta center
I = Is the second moment of area
V = Volume of the submerged portion of the body.
I just want to know how to calculate I?
Is I worked out for the entire floating board or is I worked out for just the portion of the body above the water line or is I calculated to the portion of the body below the water line?
I know that I is bd^3/12 but in my example do i use q for b and k for d - how do you know what values to use and what portion of the bosy I relates to?
Can anyone help?
Thank you.