Calico5
- 2
- 0
Hi,
I'm designing a C++ program to simulate the operation of a steel processing warehouse. Part of my code requires me to calculate the time it takes for a crane to move certain distances (mainly diagonal ones) across a large shelving rack.
The crane moves at different speeds in different directions.
Maximum x speed = 40m/min
Maximum y speed = 12.5m/min
I was thinking of using pythagoras theorem somehow to solves this (although its not required to be done this way) so:
c2 = a2 +b2
I was thinking of using:
time = distance/speed
to calculate the time for each movement in x direction and y direction. Then using pythagoras theorem on the times to get the diagonal movement time. So an example would be:
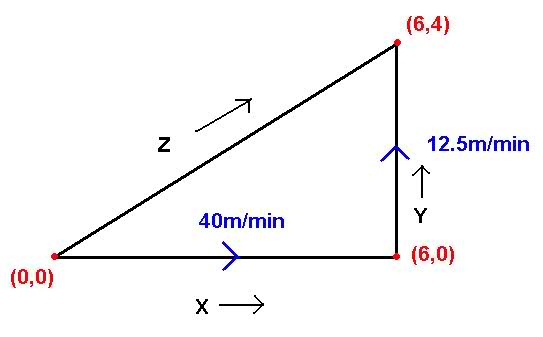
X-Time = 6/40 = 0.15min
Y-Time = 4/12.5 = 0.32min
Z-Time = SQRT(0.152+0.322) = 0.353min
Would that be correct? I am not sure if i can apply pythagoras theorem to time like that. Any Help is appreciated
Thanks
Homework Statement
I'm designing a C++ program to simulate the operation of a steel processing warehouse. Part of my code requires me to calculate the time it takes for a crane to move certain distances (mainly diagonal ones) across a large shelving rack.
Homework Equations
The crane moves at different speeds in different directions.
Maximum x speed = 40m/min
Maximum y speed = 12.5m/min
I was thinking of using pythagoras theorem somehow to solves this (although its not required to be done this way) so:
c2 = a2 +b2
The Attempt at a Solution
I was thinking of using:
time = distance/speed
to calculate the time for each movement in x direction and y direction. Then using pythagoras theorem on the times to get the diagonal movement time. So an example would be:
X-Time = 6/40 = 0.15min
Y-Time = 4/12.5 = 0.32min
Z-Time = SQRT(0.152+0.322) = 0.353min
Would that be correct? I am not sure if i can apply pythagoras theorem to time like that. Any Help is appreciated
Thanks