SimonT
- 4
- 0
Hi Members,
As described above, I am making a prototype of a vacuum and compression chamber and I could use some help calculating the wall thickness/support structure that is needed to make sure things don’t go boom.
After a fair amount of research I discovered that a few people did post making their own vacuum/compression chamber. The only problem is that the dimensions of the chambers I found on the internet were significantly smaller than the one I am attempting to make. And that the forces would be a lot bigger when using bigger dimensions.
I understand that vacuum and compression theoretically work in the same way, with 1bar = 10N/cm². With that said, it’s clear the forces occurring within the chamber depend on the quantity of the inner surface. The bigger the surface, the bigger the forces occurring.
To keep the surfaces/forces to a minimum the best way to go would be a sphere.
Because a sphere is quite difficult and expensive build, the next best thing would be a cylindrical shape. So the first prototype started to take shape, and looked something like this.
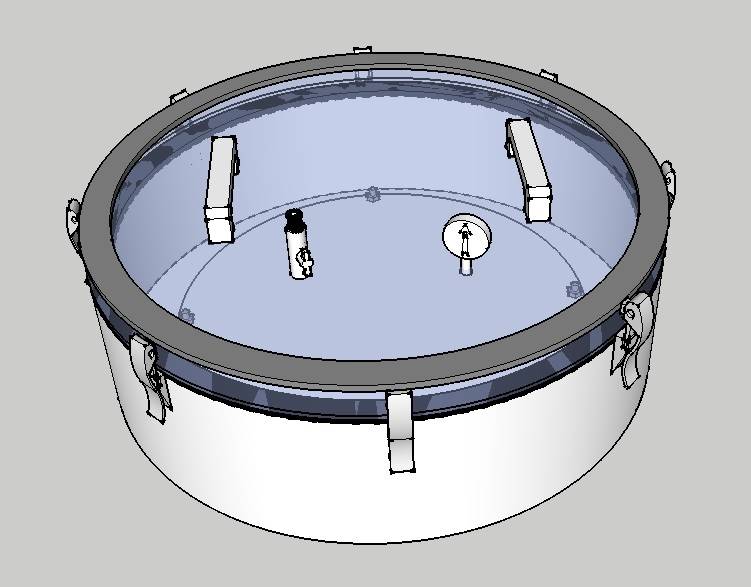
The overall idea is to create a chamber for degassing and pressurizing materials like silicones and plastics. The dimensions of the cylinder should be at least 70 cm in diameter (27,55 inches) With a height of 25cm.
Research showed that I need the chamber to withstand a maximum pressure of 3bar (43,1 psi/88,6 inHg ) for hardening the materials (product with no air bubbles). Besides that the chamber should be able to take up to 29inHg or roughly 0,98bar (14,2 psi) of vacuum to successfully degas fluids like silicones and rubbers.
So I calculated the inner surfaces of the cylinder to be able to understand the forces occurring:
Bottom and lid : π x 35cm² = 3848,45 cm² x2 = 7696,9cm²
Cylinder : 70cm x π = 219,91 cm x 25cm height = 5497,75 cm²
This creates a total of 7696,9cm² + 5497,75 cm² = 13194,65cm²
Assuming the calculations for a vacuum would be the same calc. as for pressure I considered the maximum pressure of 3 bar to be normative. In other words, if I calculate the wall thickness to withstand 3bar of pressure, pulling 29 inHg shouldn’t be a problem.
13194,65 cm² x 30N/cm² = 395839,5 Newton of force
(Short moment of silence, that the weight of a fully loaded truck! )
This is the moment I realized I would need some help on this one.
Because I already found 4mm thick stainless steel (304) material for the cylinder and the bottom I decided to start making the following (see image underneath). The prototype of the chamber changed a bit, but the overall idea stayed the same. The cylinder and bottom are already welded together, but I'm waiting for some feedback before I start welding the support structure together.
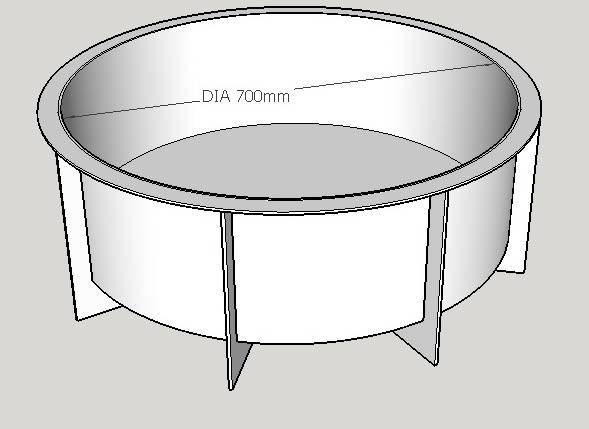
Knowing the flat areas would be the biggest problem because of the “curving” of the steel I focused on the bottom of the construction first.
I calculated the forces for only the bottom of the construction.
Bottom : π x 35cm² = 3848,45 cm² x 30N/ cm² = 115453,5 Newton of force.
Only the bottom and lid of the construction need to handle a force of roughly 11tons of weight.
I know 4mm of stainless steel simply would not do the job. The chamber needs a steel exoskeleton, welded to the steel to resist the bottom construction of curving. Mainly focusing on the center of the circle, where the “movement” would be the biggest.
I was picturing something like this.
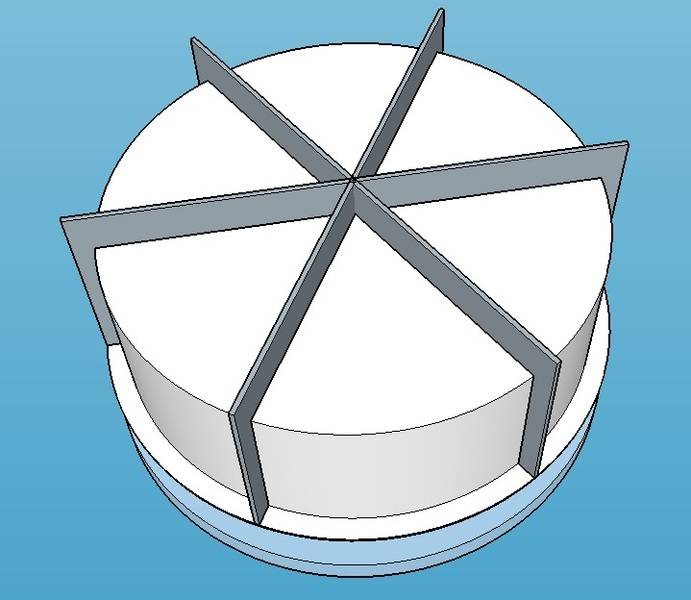
For so far I found a 8mm stainless steel (304) plate that I could use for the exoskeleton.
I do have knowledge about calculations of steel constructions, for example, calculating floor beams or roof construction isn’t a real problem. But this seems to be something slightly different, so I was hoping that someone on this forum could guide me in the right direction to determine the thickness, height and amount of support structure needed.
Besides that I was hoping someone could advise me on the thickness and material of the (if possible transparent) lid. I was thinking of Acrylic or Plexiglas. But that depends on the thickness needed (and of course of the price) A other solution would be using a similar structure as for the bottom, but then with an Acrylic or Plexiglas window.
Feel free to use everything posted above for educational purposes, your own vacuum chamber or whatever.
Greetings form the Netherlands!
As described above, I am making a prototype of a vacuum and compression chamber and I could use some help calculating the wall thickness/support structure that is needed to make sure things don’t go boom.
After a fair amount of research I discovered that a few people did post making their own vacuum/compression chamber. The only problem is that the dimensions of the chambers I found on the internet were significantly smaller than the one I am attempting to make. And that the forces would be a lot bigger when using bigger dimensions.
I understand that vacuum and compression theoretically work in the same way, with 1bar = 10N/cm². With that said, it’s clear the forces occurring within the chamber depend on the quantity of the inner surface. The bigger the surface, the bigger the forces occurring.
To keep the surfaces/forces to a minimum the best way to go would be a sphere.
Because a sphere is quite difficult and expensive build, the next best thing would be a cylindrical shape. So the first prototype started to take shape, and looked something like this.
The overall idea is to create a chamber for degassing and pressurizing materials like silicones and plastics. The dimensions of the cylinder should be at least 70 cm in diameter (27,55 inches) With a height of 25cm.
Research showed that I need the chamber to withstand a maximum pressure of 3bar (43,1 psi/88,6 inHg ) for hardening the materials (product with no air bubbles). Besides that the chamber should be able to take up to 29inHg or roughly 0,98bar (14,2 psi) of vacuum to successfully degas fluids like silicones and rubbers.
So I calculated the inner surfaces of the cylinder to be able to understand the forces occurring:
Bottom and lid : π x 35cm² = 3848,45 cm² x2 = 7696,9cm²
Cylinder : 70cm x π = 219,91 cm x 25cm height = 5497,75 cm²
This creates a total of 7696,9cm² + 5497,75 cm² = 13194,65cm²
Assuming the calculations for a vacuum would be the same calc. as for pressure I considered the maximum pressure of 3 bar to be normative. In other words, if I calculate the wall thickness to withstand 3bar of pressure, pulling 29 inHg shouldn’t be a problem.
13194,65 cm² x 30N/cm² = 395839,5 Newton of force
(Short moment of silence, that the weight of a fully loaded truck! )
This is the moment I realized I would need some help on this one.
Because I already found 4mm thick stainless steel (304) material for the cylinder and the bottom I decided to start making the following (see image underneath). The prototype of the chamber changed a bit, but the overall idea stayed the same. The cylinder and bottom are already welded together, but I'm waiting for some feedback before I start welding the support structure together.
Knowing the flat areas would be the biggest problem because of the “curving” of the steel I focused on the bottom of the construction first.
I calculated the forces for only the bottom of the construction.
Bottom : π x 35cm² = 3848,45 cm² x 30N/ cm² = 115453,5 Newton of force.
Only the bottom and lid of the construction need to handle a force of roughly 11tons of weight.
I know 4mm of stainless steel simply would not do the job. The chamber needs a steel exoskeleton, welded to the steel to resist the bottom construction of curving. Mainly focusing on the center of the circle, where the “movement” would be the biggest.
I was picturing something like this.
For so far I found a 8mm stainless steel (304) plate that I could use for the exoskeleton.
I do have knowledge about calculations of steel constructions, for example, calculating floor beams or roof construction isn’t a real problem. But this seems to be something slightly different, so I was hoping that someone on this forum could guide me in the right direction to determine the thickness, height and amount of support structure needed.
Besides that I was hoping someone could advise me on the thickness and material of the (if possible transparent) lid. I was thinking of Acrylic or Plexiglas. But that depends on the thickness needed (and of course of the price) A other solution would be using a similar structure as for the bottom, but then with an Acrylic or Plexiglas window.
Feel free to use everything posted above for educational purposes, your own vacuum chamber or whatever.
Greetings form the Netherlands!