- #1
Calculating Torque for a Rotating Cylinder
Click For Summary
Discussion Overview
The discussion revolves around calculating the torque required for a rotating solid cylinder, specifically in the context of a gearbox application. Participants explore various factors influencing torque, including surface speed, moment of inertia, and external forces acting on the cylinder.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
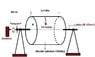
- One participant asks how to calculate the torque on an axle for a solid cylinder rotating at a surface speed of 1 m/s with a mass of 2500 kg.
- Another participant questions the meaning of the 1 m/s speed and states that if the cylinder rotates at constant angular velocity, the torque is zero.
- Some participants clarify that while torque is zero at constant speed, there is a required torque to maintain that speed due to gearbox loads and resistances.
- A participant emphasizes the need for more details about operating conditions to provide a proper answer.
- One participant provides a formula for torque based on moment of inertia and angular acceleration, but another challenges the calculation of moment of inertia and suggests using the standard formula for a solid cylinder.
- There is a discussion about how to consider acceleration timings when designing with induction motors and how that affects the required torque.
- Some participants express confusion about the moment of inertia and its role in calculating torque.
Areas of Agreement / Disagreement
Participants generally agree that torque is needed to overcome resistances and to accelerate the cylinder, but there is disagreement on the specifics of the calculations and the correct formulas to use. The discussion remains unresolved regarding the exact torque value and the correct approach to the calculations.
Contextual Notes
Participants mention various assumptions, such as the absence of external forces and the need for more details on the operating conditions. There are also unresolved issues regarding the correct moment of inertia and angular acceleration values used in the torque calculations.
- #2
- #3
Q_Goest
Science Advisor
- 3,013
- 42
You have a gearbox rotating an axle at constant speed. What external forces do you have resisting the rotation? What about the bearings? What happens to torque when axle rotation has to be accelerated?
- #4
sp1408
- 17
- 0
Didnt get your question,1m/sec is the velocity of what?
And plus if the solid cylinder rotates with constant angular velocity,the torque is zero
And plus if the solid cylinder rotates with constant angular velocity,the torque is zero
- #5
FredGarvin
Science Advisor
- 5,093
- 10
1 m/s should be the surface speed. If it's not, the number is nonsensical.
The torque to accelerate the mass is 0 at a constant speed, but due to gearbox loads and resistances, like those asked about by Q_goest, there will be a required torque to maintain a constant speed.
The OP needs to provide a lot more detail on the operating conditions before the question can be answered.
The torque to accelerate the mass is 0 at a constant speed, but due to gearbox loads and resistances, like those asked about by Q_goest, there will be a required torque to maintain a constant speed.
The OP needs to provide a lot more detail on the operating conditions before the question can be answered.
- #6
kubilayyilmaz
- 4
- 0
Ok,I have to give a lot more details for my question.
There is a solid cylinder in picture. Max Surface speed is 1m/s on the cylinder. I want to calculate how much torque of gearbox for turnnig the cylinder with 1m/s? I will use motor and gearbox for turnning the cyclinder.
So I need to torque value on the axle or output of the gearbox. When I calculate it,and then I can choose gearbox model.
There is a solid cylinder in picture. Max Surface speed is 1m/s on the cylinder. I want to calculate how much torque of gearbox for turnnig the cylinder with 1m/s? I will use motor and gearbox for turnning the cyclinder.
So I need to torque value on the axle or output of the gearbox. When I calculate it,and then I can choose gearbox model.
- #7
Q_Goest
Science Advisor
- 3,013
- 42
I'm assuming this is a project for school. Have you taken any basic physics courses yet?
There's a torque required to overcome forces resisting the rotation of the cylinder. There's also a torque required to increase the rotational velocity of the cylinder. There is no torque required above and beyond these two. You haven't mentioned any external forces acting on the cylinder, so I'll have to assume there are none. In that case, you only need torque to accelerate the cylinder so it's rotating at the speed you want, and then the only torque required is that needed to overcome any bearing resistance or possibly some very minor wind resistances, though from the looks of it you won't have any significant aerodynamic loading on this cylinder.
If you need to accelerate the mass at a certain rate, you need to consider how much torque is required to do that. Check one of these web pages:
http://theoryx5.uwinnipeg.ca/physics/rot/node5.html
http://hyperphysics.phy-astr.gsu.edu/Hbase/n2r.html
The forces on the cylinder at constant speed are going to be primarily from the bearings, but that resistance is very small. See this page for some information about rolling element bearing frictional resistance:
http://www.roymech.co.uk/Useful_Tables/Tribology/Bearing Friction.html
There's a torque required to overcome forces resisting the rotation of the cylinder. There's also a torque required to increase the rotational velocity of the cylinder. There is no torque required above and beyond these two. You haven't mentioned any external forces acting on the cylinder, so I'll have to assume there are none. In that case, you only need torque to accelerate the cylinder so it's rotating at the speed you want, and then the only torque required is that needed to overcome any bearing resistance or possibly some very minor wind resistances, though from the looks of it you won't have any significant aerodynamic loading on this cylinder.
If you need to accelerate the mass at a certain rate, you need to consider how much torque is required to do that. Check one of these web pages:
http://theoryx5.uwinnipeg.ca/physics/rot/node5.html
http://hyperphysics.phy-astr.gsu.edu/Hbase/n2r.html
The forces on the cylinder at constant speed are going to be primarily from the bearings, but that resistance is very small. See this page for some information about rolling element bearing frictional resistance:
http://www.roymech.co.uk/Useful_Tables/Tribology/Bearing Friction.html
Last edited by a moderator:
- #8
kubilayyilmaz
- 4
- 0
Thanks for your help Q_Goest.
It is not a homework. I'm a electronics eng. I have a project about the the Quality control machines. This solid cylinder is a part of the nachine.
I have looked your advised web pages and I have tried to calculate the torque with the following formulas;
Please say is it right or not ?
Torque = I (moment of inertia to the solid cylinder,rotating at Ix=Iy) x aw (a is angular acceleration)
I= 1/12.m.(3r2+h2)=1/12.2500.(3.1+2,56) = 1158,3 Nm and then
At the start and stop time
aw= a( tangential acceleration ) / r = (dV/dt)/r here I want to reach 0-1m/s in 3sec.So
aw= 1(m/s) / 1m = 1 rad/s2
Torque = 1158,3 Nm x 1 =1158,3 Nm.
Right or not?
It is not a homework. I'm a electronics eng. I have a project about the the Quality control machines. This solid cylinder is a part of the nachine.
I have looked your advised web pages and I have tried to calculate the torque with the following formulas;
Please say is it right or not ?
Torque = I (moment of inertia to the solid cylinder,rotating at Ix=Iy) x aw (a is angular acceleration)
I= 1/12.m.(3r2+h2)=1/12.2500.(3.1+2,56) = 1158,3 Nm and then
At the start and stop time
aw= a( tangential acceleration ) / r = (dV/dt)/r here I want to reach 0-1m/s in 3sec.So
aw= 1(m/s) / 1m = 1 rad/s2
Torque = 1158,3 Nm x 1 =1158,3 Nm.
Right or not?
- #9
Q_Goest
Science Advisor
- 3,013
- 42
check rotational inertia, looks wrong. for a solid cylinder, I = 1/2 MR^2. See this web page to calculate inertia:
http://hypertextbook.com/physics/mechanics/rotational-inertia/
Check angular acceleration and velocity. Final velocity is .5 rad/s so angular velocity is .5/3 = .16667
plug those into the torque equation t = I (a) shown in web pages referenced above.
http://hypertextbook.com/physics/mechanics/rotational-inertia/
Check angular acceleration and velocity. Final velocity is .5 rad/s so angular velocity is .5/3 = .16667
plug those into the torque equation t = I (a) shown in web pages referenced above.
Last edited by a moderator:
- #10
Analysis
- 52
- 0
""If you need to accelerate the mass at a certain rate, you need to consider how much torque is required to do that""
I agree the points you said But i have one querey
TOrque=I * Alpha
While designing if we consider induction motors it will behave differently.
how to consider acceleration timings alpha to get required torque?
Prakash
I agree the points you said But i have one querey
TOrque=I * Alpha
While designing if we consider induction motors it will behave differently.
how to consider acceleration timings alpha to get required torque?
Prakash
- #11
Wondermotor
- 4
- 0
look into moment of inertia. you use that to figure out your torque.
- #12
Analysis
- 52
- 0
To... wonder motor
Reply to "Look into moment of inertia you use that to find torque"
Can't understand your reply can you brief me little?
(becoz mass moment of inertia is kg m^2 from that...?)
Sorry to my late reply
Prakash
Reply to "Look into moment of inertia you use that to find torque"
Can't understand your reply can you brief me little?
(becoz mass moment of inertia is kg m^2 from that...?)
Sorry to my late reply
Prakash
Similar threads
- · Replies 12 ·
- · Replies 8 ·
Automotive
Steering Force, Determining the Lever Arm
- · Replies 9 ·
- · Replies 4 ·
- · Replies 5 ·
- · Replies 1 ·
- · Replies 7 ·