- #1
ham_revilo
- 5
- 0
Hi,
Im currently designing a small machine which uses a simple crank mechanism but my crank mechanism is not a typical one. My application:
 [/URL]
[/URL]
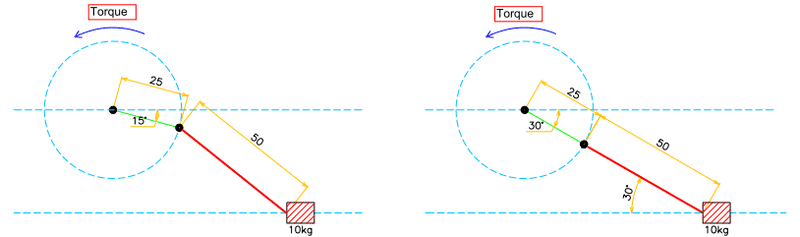
My application uses the crank wheel to drive the block (10kg). Hence, I need to calculate the torque require to drive the crank wheel. So I can select a suitable motor to do so.
The problem is my crank wheel and block is offset. Hence, it’s different from a typical crank mechanism where it’s all in a straight line.
Therefore, my question is:
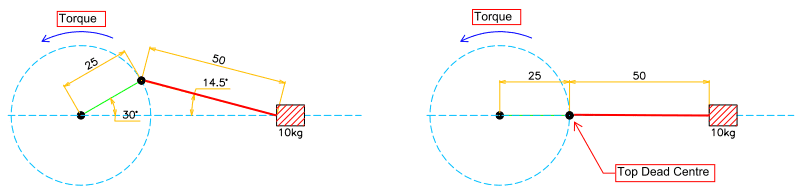
1. In my application, is there a top/bottom dead centre where torque is 0Nm since its offset?
2. If my case doesn’t have a top/bottom dead centre, how would I calculate the torque required?
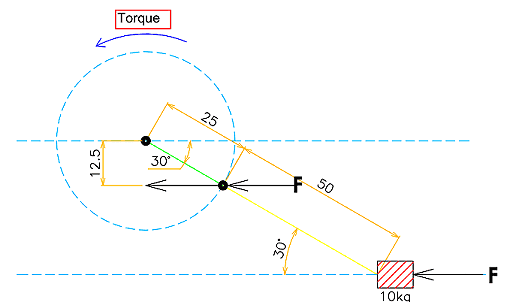
3. I came out with a theory where the Torque=F*12.5. Is it correct?
 [/URL]
[/URL]
4. If I’m wrong, Can I use the normal crank mechanism formula (Torque=F*r*sin α) to calculate the torque required?
5. How is the force reaction like so I can resolve it and calculate the torque?
Thanks in advance :)
Im currently designing a small machine which uses a simple crank mechanism but my crank mechanism is not a typical one. My application:
My application uses the crank wheel to drive the block (10kg). Hence, I need to calculate the torque require to drive the crank wheel. So I can select a suitable motor to do so.
The problem is my crank wheel and block is offset. Hence, it’s different from a typical crank mechanism where it’s all in a straight line.
Therefore, my question is:
1. In my application, is there a top/bottom dead centre where torque is 0Nm since its offset?
2. If my case doesn’t have a top/bottom dead centre, how would I calculate the torque required?
3. I came out with a theory where the Torque=F*12.5. Is it correct?
4. If I’m wrong, Can I use the normal crank mechanism formula (Torque=F*r*sin α) to calculate the torque required?
5. How is the force reaction like so I can resolve it and calculate the torque?
Thanks in advance :)
Attachments
Last edited: