Calculating Velocity and Acceleration for Circular Motion

AI Thread Summary
To calculate the velocity of a body in circular motion, one must consider the initial horizontal velocity and the effects of centripetal acceleration as it moves along the circular path. The body, with a mass of 0.24 kg and an initial velocity of 5 m/s, will maintain this speed at point B unless acted upon by external forces. The centripetal acceleration can be determined using the formula a = v²/r, where v is the velocity and r is the radius of the circular path. The tension in the string provides the necessary centripetal force, which can be calculated using F = m*a. Understanding these principles is crucial for solving problems related to circular motion.
milan666
Messages
13
Reaction score
0

Homework Statement


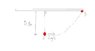
The picture shows a body of mass 0.24kg attached to a fixed point P by a light string of length 0.80m. When the body is at A, vertically below P, it is given an horizontal velocity of 5m/s as shown. It the flollows a circular path to the position B. When it is at B, calculate:
i) the velocity of the body
ii) the centripetal acceleration of the body
iii)the force exerted by the string on the body

Homework Equations


The chapter is "circular motion"



The Attempt at a Solution


I only need part i), i can manage the rest myself.
 
Physics news on Phys.org
If you could provide us a picture, I'm sure we could work some things out. :D
 
heres the pic, sorry:P
 

Attachments

  • physics.jpg
    physics.jpg
    7.9 KB · Views: 437
Thread 'Struggling to make relation between elastic force and height'

Thread 'Struggling to make relation between elastic force and height'

Hello guys this is what I tried so far. I used the UTS to calculate the force it needs when the rope tears. My idea was to make a relationship/ function that would give me the force depending on height. Yeah i couldnt find a way to solve it. I also thought about how I could use hooks law (how it was given to me in my script) with the thought of instead of having two part of a rope id have one singular rope from the middle to the top where I could find the difference in height. But the...
View full post »
Thread 'Voltmeter readings for this circuit with switches'

Thread 'Voltmeter readings for this circuit with switches'

TL;DR Summary: I would like to know the voltmeter readings on the two resistors separately in the picture in the following cases , When one of the keys is closed When both of them are opened (Knowing that the battery has negligible internal resistance) My thoughts for the first case , one of them must be 12 volt while the other is 0 The second case we'll I think both voltmeter readings should be 12 volt since they are both parallel to the battery and they involve the key within what the...
View full post »

Similar threads

Dynamics of Circular Motion
Replies
12
Views
574
Acceleration in uniform circular motion is uniform or non-uniform?
2
Replies
55
Views
3K
Relation between the velocity vector and the acceleration vector of an object
Replies
1
Views
718
Tension of string acting on stone moving in horizontal circular motion
Replies
19
Views
3K
Find the acceleration in circular motion
Replies
6
Views
2K
Friction direction change in a inclined circular bend (car on a road)
Replies
11
Views
1K
Circular Motion Questions (energies, forces, angular velocities, etc.)
Replies
2
Views
1K
A problem from a physics national competition
Replies
13
Views
1K
What actually is the centripetal acceleration formula?
Replies
28
Views
3K
A Car on a Banked Curve Moving in Uniform Circular Motion
Replies
7
Views
3K

Hot Threads

Recent Insights

Back
Top