Calculating Velocity and Distance for Ascending Double Cone on Rails

[franceboy]

Homework Statement

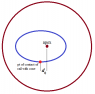
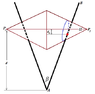
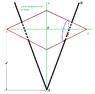
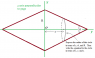
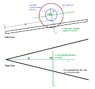
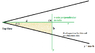
We consinder a doble cone with a radius R and an angle α (pike) and the mass m. It is located on two rails with an opening angle β. The rails enclose the angle γ with the ground. A is the lowest point of the rails.
First, the center of mass of the double cone is locatd vertically above the point A regarding the plane described by the two rails. The double cone ascends the rails. You can assume that base is in the center between the rails and that the line through the center of mass and the contact points with the rails is orthogonal to the rails.

a) Why does the double cone ascends the rails? State the conditions for the angles α,β,γ so that this happen.
b) Proof that the moment of inertia regarding the connecting line through through the pikes is I=3/10*m*R²
c) Determine the function v(d). v is the velocity of the center of mass and d is the rolled distance on the rails.
d) Calculate for the values α=50°; β=40°; γ=5°; R=10cm and m=100g the distance L which the double cone rolls on the rails and the maximal reached velocity.

Homework Equations

The Attempt at a Solution

a) The reason is that the height of the center of mass decreases while the double cone is ascending the rails. Condition: tan(γ)<tan(α/2)*tan(β/2)
b) Easy proof with the integral-formula of the moment of inertia.

However, I do not have ideas how to solve c) and d). Can you help me?

 

[gneill]

Consider conservation of energy. If you can determine the loss of gravitational PE with distance then it must go somewhere...

 

[BiGyElLoWhAt]

Well d is related to c, you can't do d without c. This actually looks like a good time for the application of some conservation laws. Or you could do some calc, but I think that can be avoided. I'm not sure, I still need to work it out.

I'm picturing something like so:

 

[franceboy]

Hi gneill,
Thank you for your help again.
Of course we have the equation: m*g*Δh_cm=1/2*m*v²+1/2*I*ω² with ω=v/r.
But i do not have a relation between h and d :(

 

[BiGyElLoWhAt]

Is there any relationship between delta h and delta L? A trigonometric relationship perhaps?

 

[franceboy]

Yeah there must be one relation but i do not how to formulate with the angles...

 

[BiGyElLoWhAt]

Look at the side view of my picture above. Draw yourself a right triangle, label the angles appropriately and it should be a simple relationship. SOHCAHTOA

 

[franceboy]

i am thinking of:
Δh=x*(tan(γ)-tan(α/2)*tan(β/2))
With x=cos(γ)*d

 

[TSny]

i am thinking of:
Δh=x*(tan(γ)-tan(α/2)*tan(β/2))
With x=cos(γ)*d

That looks good to me.

 

[franceboy]

Okay, now I have the function v(d). What about d), how can I determine L, the maximal reached distance? The maximal reached velocity is v(L), isn't it?

 

[nasu]

Well d is related to c, you can't do d without c. This actually looks like a good time for the application of some conservation laws. Or you could do some calc, but I think that can be avoided. I'm not sure, I still need to work it out.

I'm picturing something like so:

I think they mean something like this:
https://encrypted-tbn1.gstatic.com/images?q=tbn:ANd9GcQc_PS2Csv62bBTZJ6KLXM1xuXSog7RyBogHwnUwz7MA5AUljZuiQ

 

[franceboy]

Nasu, I think you are right. However, does that change any results?

 

[nasu]

No, my post was for bigyellowhat. I thought he may be confused about the geometry.
I don't think you used that picture for your calculation, did you?

 

[franceboy]

No I thought of the double cone you have presented :)

 

[TSny]

The maximum distance traveled is determined by where the double cone will no longer extend across the rails.

Note that as the cone approaches this point the radius of rolling, r, approaches zero. So, what do you expect the speed V to do as the cone approaches this point?

 

[franceboy]

If the radius of rolling approaches zero, the velocity must be zero!
That means I have to solve the equation v(L)=0 and than integrate the function v(d) from zero until L. Is that right? But the function v(d) does not become zero except for d=0

 

[TSny]

You should be able to determine L from the geometry.

You then find that v(d) goes to zero at d = L.

 

[franceboy]

My idea is to look when Δh=R.
Another idea is to look when the double cone would drop between the rails: R/tan(α/2)<tan(β/2)*d
Is one of the ideas right? Why is the v(d)=0 at this point?

 

[TSny]

My idea is to look when Δh=R.
Another idea is to look when the double cone would drop between the rails: R/tan(α/2)<tan(β/2)*d
Is one of the ideas right? Why is the v(d)=0 at this point?

You are right that v(d) is not zero at the point where the cone drops between the rails.

[EDIT: I now think v(d) = 0 at that point. Ugh!]

 

[BiGyElLoWhAt]

Hmmm... Is double cone a standard geometric shape? I guess I'm just not familiar with it, I actually googled it before I posted that picture (doh!). Stupid google, leading me astray.

And as far as the recent posts go, I think it makes physical sense that v is non zero at d=L. Why would the mass stop moving if it still has GPE w.r.t. the zero of your system? (if the center of mass is free to move down, neglecting friction, it will)

 

[franceboy]

So, is this equation: R/tan(α/2)=tan(β/2)*L right? Is v maximal the velocity after the distance of L: v(L)?

 

[TSny]

So, is this equation: R/tan(α/2)=tan(β/2)*L right?

This would be correct if L is measured from point A where the two rails meet. The question seems to define the distance d as the distance rolled. At the starting position, the point of contact of the cone with the rails is already some distance, D say, from A. So, if L is meant to be the maximum distance rolled from the starting point, then you would need to subtract D from your expression for L. This has caused some confusion for me.

[EDIT: Sorry, I had the initial position drawn incorrectly. The initial point of contact is at A and the CM is vertically above A, so there is no offset distance D. Your expression for L looks correct to me.]

Is v maximal the velocity after the distance of L: v(L)?

According to what I'm getting, the maximum velocity is not at the distance L. I believe the maximum velocity occurs well before L. After rechecking my work, I am again getting that v approaches zero as d approaches L.

I have been trying to really convince myself that it is OK to use v = ωr where r is the radius of the instantaneous cross section of the cone at the point of contact. If you painted a stripe on the cone corresponding to the points of contact of the cone with one of the rails, you would get a "helical" stripe of decreasing radius. The cone is rolling on this stripe. It is not rolling on a circular cross section. I need to think some more about the relation between v and ω.

 

[franceboy]

Well, I think I did not express myself very well. d is meant as the translation distance of the center of mass. So, my equation is right, isn´t it?.
I did not get, why v(L)=0. What happened to the potential energy?
I worked in c) with ω=v/R and I got:
v(d)=√(20/13*g*tan(γ)*d) Is that wrong?
How did you determine the maximal distance L?

 

[TSny]

Well, I think I did not express myself very well. d is meant as the translation distance of the center of mass. So, my equation is right, isn´t it?.

Yes, your equation is correct.

I did not get, why v(L)=0. What happened to the potential energy?

L is the position where r = 0. So, V = ωr = 0 at that point.

When r = 0, The potential energy has been entirely converted to rotational KE.

I worked in c) with ω=v/R and I got:
v(d)=√(20/13*g*tan(γ)*d) Is that wrong?
How did you determine the maximal distance L?

I assumed ω=v/r where the radius of rotation, r, decreases as the cone moves. r depends on d, R, and the angles α and β. I end up with a more complicated expression for v(d) that includes the angles α and β and the radius R. Did you derive an expression for r in terms of d, R, α and β?

I agree with your expression for L. L = R/[tan(α/2)*tan(β/2)]

 

[franceboy]

I always thought that the radius R is the same as r. How can a body rotate with another radius r?
No I do not have a expressions for r. In school we did not learn that r is not R. Do you understand what I mean?

 

[TSny]

As shown in the picture, r decreases as the cone moves along the rails.

 

[franceboy]

As shown in the picture, r decreases as the cone moves along the rails.

Thank you for the sketch.
r must be something like r=R-h-sin(y)*d with h as the difference of the height of the center of mass. But the conversation of energy is still right: m*g*h=1/2*m*v^2+1/2*I*w^2 and w=v/r and h=cos(y)*d*(tan(y)-tan(a/2)*tan(b/2))
Sorry, that I did not write the greek letters. I can not work with the "new" forum, yet.

 

[franceboy]

So if my consideration is right, I have to to look for a local maximum of the function v(d) with 0<d<L.
Is that right TSny?

 

[TSny]

So if my consideration is right, I have to to look for a local maximum of the function v(d) with 0<d<L.
Is that right TSny?

Yes, you'll have to find where v(d) is maximum. I get a fairly messy expression for v(d).
Solving v'(d) = 0 algebraically appears to lead to solving a cubic equation in d.

 

[franceboy]

Are the equations in post 27 right? Then the function v(d) and v'(d) appear very complicated...