Calculating Velocity when Stuntman Jumps from 1.25m Height

[Istiak]

Homework Statement

A stuntman jumped from $1.25 \ \text{m}$ height and, landed at distance $10 \ \text{m}$. Find velocity when he jumped. (Take $\text{g}=10 \ ms^{-2}$)

Relevant Equations

$$h=\frac{1}{2}gt^2$$

>

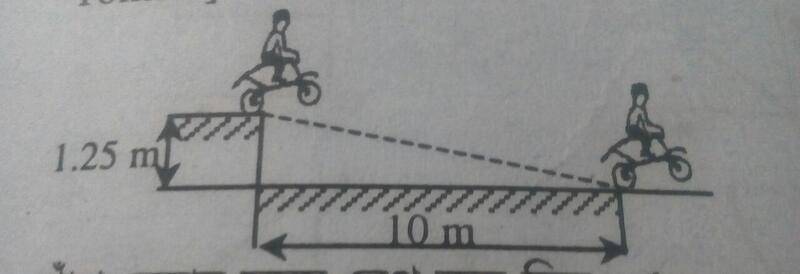
>A stuntman jumped from $1.25 \ \text{m}$ height and, landed at distance $10 \ \text{m}$. Find velocity when he jumped. (Take $\text{g}=10 \ ms^{-2}$)

I had solved it following way.

$$h=\frac{1}{2}gt^2$$
$$=>1.25=5\cdot t^2$$
$$=>t=\frac{1}{2}$$
And, $$s=vt$$
$$v=\frac{s}{t}$$
$$=\frac{10 \ m}{\frac{1}{2} \ s}$$
$$=20 \ m/s$$

The answer is correct (checked from book answer). But, $v$ is average speed in the following equation.

$$s=vt$$

But, they told me to find initial velocity. That's why I think my answer is correct but, method is wrong so, the whole work is wrong either.

 

[PeroK]

There's an assumption here that he jumped horizontally.

You've used, perhaps without realising, that the horizontal component of the velocity is constant.

Use those to get the right answer for the right reason!

 

[PeroK]

PS you need to include units in your working. E.g. $20m/s$

 

[Istiak]

You've used, perhaps without realising, that the horizontal component of the velocity is constant.

That should be 9.8 m/s but, which formula I should use?

 

[PeroK]

That should be 9.8 m/s but, which formula I should use?

Where did $9.8m/s$ come from? Formula for what?

 

[Istiak]

Where did $9.8m/s$ come from? Formula for what?

9.8 from Gravitational acceleration. Formula for solving that problem

 

[PeroK]

9.8 from Gravitational acceleration. Formula for solving that problem

I don't understand what you are asking. Do you know what vector components are?

 

[Istiak]

Do you know what vector components are?

Yes! Ohh! I have to use Vector.

 

[Istiak]

@PeroK I was trying to find distance of hypotenuse.
$$c=\sqrt{a^2+b^2}$$
$$=\sqrt{10^2 \ m+1.25^2 \ m}$$
$$=10.0778 \ m$$
I was thinking that initial velocity is $$0 \ ms^{-1}$$ since, that stuntman started his bike in initial position. Hence, initial velocity is $$0$$. But, OP says that I have to find initial velocity. How can I find? I was claiming that final velocity is $$0$$. But, If I use $$v^2=u^2+2gh$$ than, I get initial velocity is negative which isn't. So, what should I do with distance of that stuntman was "flying"?

 

[PeroK]

We need to see some vector components of velocity.

 

[Delta2]

Your method is correct and your answer is correct, however it seems to me that you haven't realized some things:

1. when you write $s=vt$, s is the horizontal distance and v is the horizontal component of the initial velocity (and it happens to be that the initial velocity has only horizontal component but it could have been different), which does not change through the motion, that's why we can write $s=vt$ after all, this equation is when the velocity is constant (or when the velocity is the average velocity but this is not the case here).
2. The trajectory of the cyclist will be parabolical. In any case it won't be the hypotenuse (dotted line).
3. The total velocity of the cyclist during the parabolical trajectory changes both in magnitude and direction, however the horizontal component of the total velocity remains constant. It is the vertical component that keeps changing.

 

[Delta2]

@Istiakshovon let me please ask you something: Why do you think the horizontal component of velocity remains constant through out the motion?

 

[Istiak]

@Istiakshovon let me please ask you something: Why do you think the horizontal component of velocity remains constant through out the motion?

Cause, gravitational force is pulling.

 

[Delta2]

Cause, gravitational force is pulling.

you need to be more precise than that. Ok gravitational force is pulling so what?

 

[Istiak]

you need to be more precise than that. Ok gravitational force is pulling so what?

gravitational force is pulling and, gravitational force is constant. Hence, horizontal component of velocity remains constant (To my mind, it's not constant completely cause, $v$ is increasing per sec).

 

[Istiak]

Isn't that correct?

 

[Delta2]

Nope its not because gravitational force is constant.

 

[Istiak]

Nope its not because gravitational force is constant.

So, that's constant how?

 

[Delta2]

A velocity component remains constant if the net force in the direction of that component is zero (that is a corollary from Newton's 2nd law). So do we have a net force in the horizontal direction?

 

[Istiak]

do we have a net force in the horizontal direction?

If you are asking at t=0 s than, I will say, "yes" (I meant no. But, we have which is 0 N). Cause, at t=0 s only gravitational force is pulling that cyclist. hence, net force at t=0 is 0.

 

[PeroK]

So, that's constant how?

Reading your posts on this thread gives me no confidence that you understand what a vector is. Your knowledge of the laws of motion seems limited to one dimensional motion.

You need to prove me wrong!

 

[PeroK]

If you are asking at t=0 s than, I will say, "yes" (I meant no. But, we have which is 0 N). Cause, at t=0 s only gravitational force is pulling that cyclist. hence, net force at t=0 is 0.

And this gives me no confidence that you understand the concept of a gravitational force!

 

[Delta2]

If you are asking at t=0 s than, I will say, "yes" (I meant no. But, we have which is 0 N). Cause, at t=0 s only gravitational force is pulling that cyclist. hence, net force at t=0 is 0.

ok so we can agree that the net horizontal force at t=0 is 0. What about t=0.1 is there any net horizontal force?What about any t? is there any net horizontal force?

 

[Istiak]

You need to prove me wrong!

How can I? You know more than me :D .

Your knowledge of the laws of motion seems limited to one dimensional motion.

Maybe, yes maybe, no. I am saying no, cause I had lot of problems of two dimensional motion earlier (that was lot of time ago nearly 7-8 months).

 

[Istiak]

is there any net horizontal force?

Yes

 

[Delta2]

Yes

I disagree with this but why do you say yes , which is this horizontal force you see?

 

[Istiak]

I disagree with this but why do you say yes , which is this horizontal force you see?

sh*t! When I saw the message then, I was thinking that I am confusing with horizontal and, vertical. After using Google Translate, I am now sure that I was confused of horizontal and vertical axis. Now, I understand. Usually, I was talking about Vertical axis not Horizontal. :( . And, Sorry to disturb. Thanks to clear my confusion. :)

 

[Istiak]

I was mistaking another thing which is vertical force exists at t=0 s either. That's not 0 at t=0 s.

 

[Delta2]

I was mistaking another thing which is vertical force exists at t=0 s either. That's not 0 at t=0 s.

yes the vertical force is not zero at all times, not only t=0. It is equal to the gravitational force.

 

[Istiak]

And, horizontal force is 0 N. But, If I think of hypotenuse then, there is force (maybe there is no force where hypotenuse ends).