Calculating water pressure, gauge pressure

[mm2424]

Homework Statement

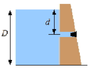
I've attached an image of a dam. The problem reads as follows: The fresh water behind a reservoir dam has depth D = 15 m. A horizontal pipe 4 cm in diameter passes through the dam at depth d = 6 m. A plug secures the pipe opening. Find the magnitude of the frictional force between the plug and the pipe wall.

Homework Equations

gauge pressure = ρgd

The Attempt at a Solution

The answer to this problem seems to entail calculating the gauge pressure and then multiplying it by the area of the pipe to get the force of the water on the plug. I have three questions:

1) Why do we not consider the air pressure above the water here as opposed to only the gauge pressure (ρgd)? Is it because the water in the pipe is not below the air, but rather below rock? I'm not really clear on whether air pressure can only act downward or whether it can "sneak" into crevices like those created by the pipe.

2) If this problem instead involved a giant basin with a plug in the bottom, would we then have to consider the air pressure?

3) I initially tried to approach this problem using Bernoulli's equation, with the velocities equal to 0 on both side. I then realized that Bernoulli's equation reduces to the standard water pressure equation when the fluids aren't moving. Is it fair to say this is true?

Thanks a million!

Homework Statement

Homework Equations

The Attempt at a Solution

 

[Delphi51]

Air pressure acts equally on both sides, so it can be ignored.

 

[mm2424]

Oh, I see. I didn't even think about how the air is exerting a pressure on the OTHER side of the plug. But with regard to my other question, I assume based on your answer that it's fair to say that the air pressure still exerts an effect on the water in the pipe. It's a bit hard for me to understand how the pressure of the air "squeezes" into the pipe, but I've accepted that none of this stuff is intuitive to me :).

 

[Delphi51]

Yah, pressure is strange. It pushes equally in all directions and certainly squeezes into every possible recess. Scuba divers are very familiar with the idea of air pressure adding onto pressure due to the weight of water above them. 33 feet (11 meters) of water equals one atmosphere of pressure. So the pressure on the outside of your body is 2 atmospheres at that depth. You must breath air from your tank at that same pressure or you won't breathe at all!