Calculating Work Done in Moving Multiple Charges in a Cube Configuration

[cupid.callin]

The question is like this:

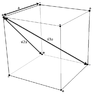
8 charges of magnitude q and different sighs are placed at corners of a cube of side a.
Find the work done in taking them far away from each other.

Homework Equations

U = kq₁q₂/r
W = ΔU

The Attempt at a Solution

First i found out the potential energy of a +q charge

U = -3kq²/a + 3kq²/√2a - Kq²/√3a

and the same comes out to be for -q charge (of course)

So for 1 charge,
W = U_f - U_i
W = 0 - ( -3kq²/a + 3kq²/√2a - Kq²/√3a )

W = 3kq²/a - 3kq²/√2a + Kq²/√3a

So work done for 8 charges = 8W ... Right?

But its wrong.

Some help please.

 

[gneill]

Each time you remove a charge from the group you get less work than from the last one because there are fewer and fewer charges contributing to the field.

The same thing happens in reverse, too, when you assemble charges. The first one is free -- no competing charge to work against or be attracted to. The next one sees the first charge, so there's work to be done. The next one after that sees both of the first two, and so on.

 

[cupid.callin]

well what if i take all of them together?

initial U for all is same.

and obviously we won't consider value of U in b/w the process

...

So then shouldn't work done be 8W?

 

[gneill]

well what if i take all of them together?

initial U for all is same.

and obviously we won't consider value of U in b/w the process

...

So then shouldn't work done be 8W?

The work done (or gained back) to take the arrangement apart will the the negative of the work done to assemble it in the first place. Either way, you need to calculate the sum of all the individual works.

I suppose you could work out how the potential changes when the cube is scaled by some factor, and then integrate from 1 to infinity. But that's going to require even more brain sweat than just calculating the work done assembling the cube one charge at a time.

 

[cupid.callin]

i'll try your way and get back on this asap