singleton
- 119
- 0
Calculus maxima and minima word question...can't understand :(
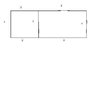
A rectangular field is going to be enclosed and divided into two separate rectangular areas (not equal either). Find the minimum fencing required if the total area of the field is 1200m^2
(See the picture attached right now)
My answer so far:
Let x represent the width of the rectangular area's width in metres
Let y represent the length of the first rectangular area in metres
Let z represent the length of the second rectangular area in metres
I've identified that we want to minimize the total amount of fencing P
So the function is:
P = 3x + 2y + 2z
Given the total area = area of first rectangle + area of second rectangle
1200 = xy + xz
The only problem is that I have three variables and I think I'm supposed to somehow do this with two as we've only been taught how to use two so far. I could figure it out with two but I don't know what is wrong with my answer so far :( Have I wrongly interpreted the question?
thanks for any help!
A rectangular field is going to be enclosed and divided into two separate rectangular areas (not equal either). Find the minimum fencing required if the total area of the field is 1200m^2
(See the picture attached right now)
My answer so far:
Let x represent the width of the rectangular area's width in metres
Let y represent the length of the first rectangular area in metres
Let z represent the length of the second rectangular area in metres
I've identified that we want to minimize the total amount of fencing P
So the function is:
P = 3x + 2y + 2z
Given the total area = area of first rectangle + area of second rectangle
1200 = xy + xz
The only problem is that I have three variables and I think I'm supposed to somehow do this with two as we've only been taught how to use two so far. I could figure it out with two but I don't know what is wrong with my answer so far :( Have I wrongly interpreted the question?
thanks for any help!